Delta-x-Methode
| Fassen wir noch einmal alles, was du an diesem Beispiel lernen solltest, zusammen:
Der Differenzenquotient beschreibt die mittlere (durchschnittliche) Änderungsrate innerhalb eines Intervalls von |
Von der mittleren Änderungsrate ist die sogenannte lokale Änderungsrate zu unterscheiden. Im nächsten Beispiel wollen wir klären, was man unter dem Begriff der lokalen Änderungsrate versteht, und wie sie berechnet wird.
7. Bsp.:Brücke
Eine Brücke folgt einem parabelförmigen Bogen. Legt man den Ursprung des Koordinatensystems genau senkrecht unter den höchsten Punkt der Brücke hat diese Parabel die Gleichung 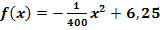 mit x
mit x  [-50;50]. Dabei gibt
[-50;50]. Dabei gibt 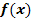 die Höhe über dem Erdboden in Metern an. Vergleiche dazu die folgende Abbildung! Ein Fußgänger überquert diese Brücke;er geht dabei von Punkt A(-50|0) über B(0|6,25) zu C(50|0).
die Höhe über dem Erdboden in Metern an. Vergleiche dazu die folgende Abbildung! Ein Fußgänger überquert diese Brücke;er geht dabei von Punkt A(-50|0) über B(0|6,25) zu C(50|0).
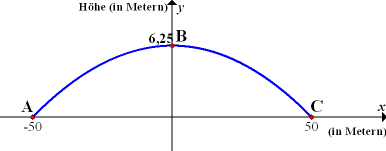
Abb.: Graph der Parabel 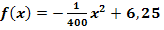 mit x
mit x  [-50;50]
[-50;50]
a.) Berechne die absolute Höhenänderung, also den absoluten Höhenunterschied (in Metern), den der Fußgänger zwischen den Punkten A und B überwindet!
b.) Berechne die mittlere (durchschnittliche) Höhenänderung des Fußgängers, also die durchschnittliche Steigung der Brücke, zwischen den Punkten A und B! (Dies kann man auch als mittlere Änderungsrate der Höhe 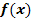 im Intervall von
im Intervall von 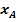 bis
bis 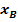 bezeichnen.)
bezeichnen.)
c.) Auf seinem Weg von A nach B passiert der Fußgänger der Reihe nach unteranderem die Punkte 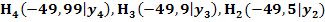 und
und 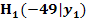 . Berechne die durchschnittliche Steigung der Brücke, zwischen den Punkten A und
. Berechne die durchschnittliche Steigung der Brücke, zwischen den Punkten A und 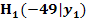 , den Punkten A und
, den Punkten A und 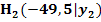 , den Punkten A und
, den Punkten A und 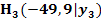 sowie Punkten A und
sowie Punkten A und 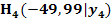 . Ermittle dann durch Grenzübergang, welche Steigung die Brücke genau im Punkt A hat! (Die Steigung in einem bestimmten Punkt kann man auch als lokale Änderungsrate der Höhe
. Ermittle dann durch Grenzübergang, welche Steigung die Brücke genau im Punkt A hat! (Die Steigung in einem bestimmten Punkt kann man auch als lokale Änderungsrate der Höhe 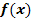 bezeichnen.)
bezeichnen.)
Lösung:
Zu 7a.)
Die Koordinaten der Punkte A und B sind bereits angegeben:
A(-50|0) und B(0|6,25)
Wegen 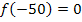 befindet sich der Fußgänger im Punkt A noch auf Höhe des Erdbodens.
befindet sich der Fußgänger im Punkt A noch auf Höhe des Erdbodens.
Wegen 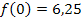 befindet sich der Fußgänger im Punkt B in 6,25 m über dem Erdboden.
befindet sich der Fußgänger im Punkt B in 6,25 m über dem Erdboden.
Der absolute Höhenunterschied berechnet sich natürlich mit 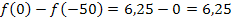 und beträgt somit 6,25 m. Das ist hoffentlich klar. Dazu hätte man eigentlich gar keine Rechnung gebraucht;das sieht man ja schon in der Abbildung.
und beträgt somit 6,25 m. Das ist hoffentlich klar. Dazu hätte man eigentlich gar keine Rechnung gebraucht;das sieht man ja schon in der Abbildung.
Wir halten fest:Der absolute Höhenunterschied zwischen zwei Punkten 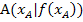 und
und 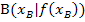 kann auch als absolute Wertänderung der Funktion
kann auch als absolute Wertänderung der Funktion 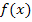 bezeichnet werden.
bezeichnet werden.

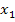 bis
bis 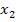 . Darunter versteht man die Veränderung des Funktionswertes
. Darunter versteht man die Veränderung des Funktionswertes 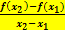 .
.