Delta-x-Methode
Es soll die Gleichung der Tangente im Punkt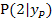 
an die Funktion 
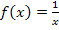berechnet werden. (Wir brauchen sie später bei der Berechnung des y-Achsenabschnitts t.) Da eine Tangente eine Gerade ist, gilt für sie auch die allgemeine Geradengleichung y = mx + t, mit der Steigung m und dem y-Achsenabschnitt t.
Als erstes berechnen wir die y-Koordinate des Punktes P. Weil P ein Punkt des Graphen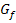 
ist, erhalten wir seine y-Koordinate, indem wir die x-Koordinate von P in die Funktionsgleichung 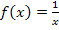einsetzen:
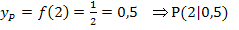
Als nächstes müssen wir die Steigung m der Tangente im Punkt P ermitteln. Die Tangentensteigung erhalten wir durch Einsetzen von x = 2 in die Ableitung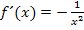 
. Es gilt somit für die Tangentensteigung:
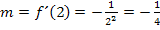
Den y-Achsenabschnitt t erhält man, wenn man die Koordinaten des Punktes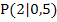 
für x bzw. y und den soeben berechneten Wert für m einsetzt und nach t auflöst.
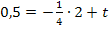
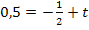
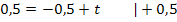
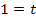
Die Gleichung der Tangente im Punkt P lautet daher: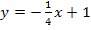 
Fertig!
Kleiner Hinweis:
Schreibt man übrigens statt 
den Buchstaben h, kommt man zur sogenannten h-Methode. Dies ist im Prinzip das gleiche wie mit , nur dass man eben h statt schreibt.
In den nächsten Beispielen wollen wir uns mit Anwendungsaufgaben des Differenzen- und des Differenzialquotienten beschäftigen. Für Schüler einer 11. Klasse des G8 ist dies besonders wichtig. Die Begriffe Differenzen- und Differenzialquotient lassen sich ja anschaulich nicht nur als Sekanten- und Tangentensteigung deuten, sondern auch als „mittlere Änderungsrate“ und „lokale Änderungsrate“. Was die Begriffe „mittlere Änderungsrate“ und „lokale Änderungsrate“ genau bedeuten, wird an Hand der folgenden Beispiele herausgearbeitet.
6. Bsp.:Wertentwicklung einer Aktie
Der folgende Graph zeigt die Wertentwicklung einer Aktie seit Öffnung der Börse um 8 Uhr bis zum Schluss der Börse um 16 Uhr. x ist die Zeit in Stunden seit Öffnung der Börse. 
ist der Wert der Aktie in €.
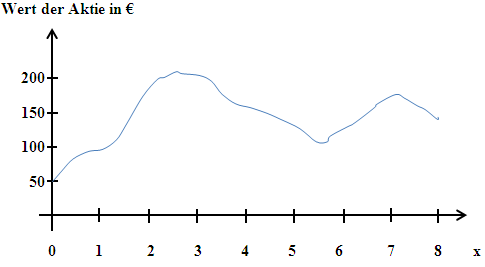
In der folgenden Tabelle kannst du den Wert der Aktie jeweils zur vollen Stunde ablesen:
| x in Std. | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Wert f(x) in € | 50 | 98 | 182 | 198 | 169 | 146 | 139 | 172 | 152 |
a.) Berechne die absolute Wertänderung in € zwischen 9 und 11 Uhr, sowie zwischen 10 und 15 Uhr!
b.) Die mittlere Wertänderung erhält man, indem man die absolute Wertänderung durch die vergangene Zeit dividiert, d.h. die Wertänderung im Verhältnis zur Zeit angibt. Berechne die mittlere Wertänderung zwischen 9 und 11 Uhr sowie zwischen 10 und 15 Uhr!
