Herleitung der Tangentensteigung aus der Sekantensteigung mittels des Differenzialquotienten
Gegeben ist eine Funktion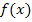 
, beispielsweise die Normalparabel 
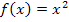. Wir suchen die Steigung der Funktion in einem bestimmten Kurvenpunkt 
.
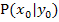Dabei steht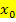 
immer für die x-Koordinate eines festen Punktes P des Graphen.
Unterscheide genau zwischen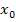 
und x! Mit 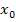ist grundsätzlich eine bestimmte, feste Zahl gemeint, wogegen x eine Variable, also nicht fest gelegte Zahl ist.
Sagen wir ´mal, der gegebene Kurvenpunkt P lautet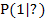 
. Er hat dann also die x-Koordinate 
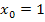. In anderen Worten: 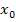ist einfach die x-Koordinate des angegebenen Kurvenpunktes.
Weil P ein Punkt des Graphen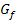 
ist, kann seine y-Koordinate leicht berechnet werden, indem man seine x-Koordinate in 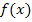einsetzt. Es gilt also 
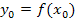und in unserem Beispiel 
.
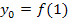Wir wollen nun die Steigung der Normalparabel 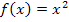, also die Steigung der Tangente an 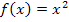, im Punkt 
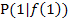ermitteln.
Im Folgenden wird an diesem Beispiel ausführlich erklärt, wie man die Steigung einer Kurve in einem bestimmten Kurvenpunkt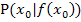 
berechnet. Bisher haben wir ja nur die Steigung m von Geraden kennengelernt. Eine Gerade hat in jedem Kurvenpunkt die gleiche Steigung;sonst wäre es ja keine Gerade. Wie aber berechnet man nun die Steigung einer Kurve? Diese Steigung ändert sich natürlich von Punkt zu Punkt. Die Normalparabel ist ja an manchen Stellen steiler als an anderen. An manchen Stellen fällt, an anderen Stellen steigt sie und im Scheitel verläuft die Tangente an die Parabel sogar waagrecht. Die Steigung einer Kurve hängt also vom jeweiligen Kurvenpunkt P ab. Die Steigung der Funktion entspricht, wie gesagt, immer der Steigung der Tangente an den Funktionsgraph in diesem Punkt. Da eine Tangente den Funktionsgraphen in der näheren Umgebung aber ausschließlich im Punkt P berührt, haben wir nur einen einzigen Punkt der Tangente gegeben. Doch braucht man eigentlich ja zwei Punkte, um die Steigung einer Geraden berechnen zu können. Was also tun?
Grundsätzliches Vorgehen bei der Berechnung der Tangentensteigung im Punkt P:
Wir wählen zuerst – zusätzlich zum gegebenen Punkt P – einen Hilfspunkt H, der ebenfalls auf dem Graphen und in der Nähe von P liegt. Durch die beiden Punkte P und H ist nun die Gerade PH eindeutig festgelegt. Diese Gerade ist natürlich keine Tangente, sondern eine Sekante des Graphen, da sie den Graphen in den zwei Punkten P und H schneidet. Mit Hilfe der zwei Punkte P und H lässt sich zumindest die Steigung der Sekante PH leicht berechnen. Danach schieben wir den Hilfspunkt H in Gedanken beliebig nah an P heran. So wird aus der Sekante letztendlich die Tangente und wir können von der Sekantensteigung auf die Tangentensteigung schließen. Soweit unser Plan. Jetzt müssen wir das aber konkret in die Tat umsetzen.
