Herleitung der Tangentensteigung aus der Sekantensteigung mittels des Differenzialquotienten
Trotzdem solltest du dich fragen, ob du noch weißt, wie man die Gerade 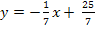 mit Hilfe der Steigung m und dem y-Achsenabschnitt t in ein Koordinatensystem zeichnen kann. Zugegeben, der y-Achsenabschnitt ist hier eine „blöde“ Zahl. Du musst die Gerade ja nicht wirklich zeichnen, sondern nur überlegen, wie es funktionieren würde. Weißt du es noch? Den y-Achsenabschnitt t geht man auf der y-Achse nach oben bzw. nach unten, je nach dem ob t positiv oder negativ ist. In diesem Fall müsste man also vom Ursprung (Nullpunkt) aus um
mit Hilfe der Steigung m und dem y-Achsenabschnitt t in ein Koordinatensystem zeichnen kann. Zugegeben, der y-Achsenabschnitt ist hier eine „blöde“ Zahl. Du musst die Gerade ja nicht wirklich zeichnen, sondern nur überlegen, wie es funktionieren würde. Weißt du es noch? Den y-Achsenabschnitt t geht man auf der y-Achse nach oben bzw. nach unten, je nach dem ob t positiv oder negativ ist. In diesem Fall müsste man also vom Ursprung (Nullpunkt) aus um 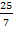 nach oben gehen. Hier schneidet die Gerade die y-Achse. Das wusstest du sicher noch. Doch wie war das noch ´mal mit dem Steigungsdreieck?
nach oben gehen. Hier schneidet die Gerade die y-Achse. Das wusstest du sicher noch. Doch wie war das noch ´mal mit dem Steigungsdreieck?
Vom Schnittpunkt mit der y-Achse ausgehend geht man den Nenner der Steigung immer nach rechts und den Zähler von m nach oben, wenn m positiv ist, bzw. nach unten, wenn m negativ ist. So erhält man einen zweiten Geradenpunkt. Damit lässt sich die Gerade dann leicht zeichnen.
Bitte merke dir das mit dem Steigungsdreieck gut! Immer den Nenner nach rechts und den Zähler nach oben (+) bzw. unten (-) gehen. Als Merkhilfe sollen die beiden e´s in den Worten „Nenner“ und „rechts“ dienen. Du wirst das noch oft in der Zukunft brauchen können.
| Hier noch einmal alles Wichtige, was du an diesem Beispiel lernen solltest, kurz zusammengefasst:
Gegeben ist eine Funktionsgleichung · y-Koordinaten der Kurvenpunkte ermitteln, indem man jeweils die x-Koordinate in · Sekantensteigungmit der Formel · Berechneten Wert für die Steigung m in die allgemeine Geradengleichung · Zusätzlich zu m für x und y die Koordinaten eines Kurvenpunktes einsetzen, um den y-Achsenabschnitt t zu berechnen · Berechnete Werte für m und t in die allgemeine Geradengleichung |
Um die Steigung einer Kurve in einem bestimmten Punkt zu ermitteln, muss in diesem Punkt die Tangente an den Funktionsgraphen gelegt und die Steigung dieser Tangente berechnet werden. Die Steigung einer Kurve entspricht nämlich grundsätzlich der Steigung der Tangente.
Aber wie kommt man jetzt von der Sekantensteigung zur Tangentensteigung? Das schauen wir uns am besten an einem konkreten Beispiel an.
Einführungsbeispiel zur Berechnung der Tangentensteigung:

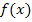 . Um die Gleichung der Sekante durch die Kurvenpunkte
. Um die Gleichung der Sekante durch die Kurvenpunkte 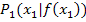 und
und 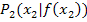 zu berechnen, geht man folgendermaßen vor:
zu berechnen, geht man folgendermaßen vor: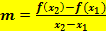 berechnen
berechnen  einsetzen
einsetzen