Herleitung der Tangentensteigung aus der Sekantensteigung mittels des Differenzialquotienten
Entsprechend bedeutet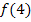 
, dass für x in die Funktion 
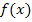die x-Koordinate 
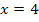eingesetzt werden soll. 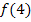ist daher die y-Koordinate des Kurvenpunktes 
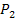. Die Kurvenpunkte kann man somit auch in der Form 
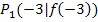und 
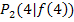schreiben. Ohne gleich die oben konkret berechneten y-Koordinaten einzusetzen, kann man die Sekantensteigung daher auch folgendermaßen schreiben:
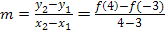
Den Ausdruck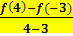 
nennt man in diesem Zusammenhang den „Differenzenquotient“ der Funktion 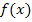zu den Punkten 
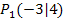und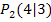 
. Es handelt sich schließlich insgesamt um einen Quotienten und im Zähler sowie im Nenner steht eine Differenz.
Durch den Ausdruck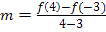 
wird die Sekantensteigung m zu den Kurvenpunkten 
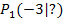und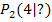 
beschrieben. Der Differenzenquotient 
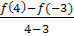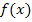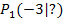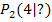gibt also die Steigung der Sekante zur Funktion durch die Kurvenpunkte und an.
Allgemein können wir festhalten:Die Steigung der Sekante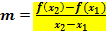 
wird als Differenzenquotient der Funktion 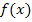zu den Kurvenpunkten 
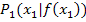und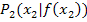 
bezeichnet.
Nun wieder zurück zu unserem Beispiel:
Wir haben oben die Sekantensteigung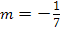 
berechnet. Wir setzen jetzt den berechneten Wert für m in die allgemeine Geradengleichung 
ein. Die Sekante 
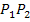hat also eine Gleichung der Form: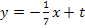 
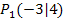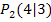Um den y-Achsenabschnitt t zu berechnen, müssen für x und y die Koordinaten eines der beiden Punkte oder in 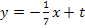eingesetzt werden. Welchen Punkt man dabei verwendet, ist egal. Du darfst aber keinesfalls die x-Koordinate des einen und die y-Koordinate des anderen Punktes nehmen! Entscheide dich also für einen der zwei Punkte! Wir verwenden hier den Punkt 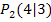, da er positive Koordinaten hat.
y-Achsenabschnitt t berechnen:
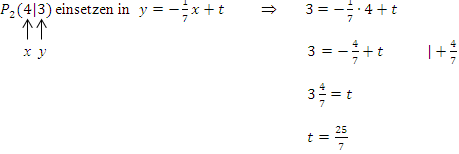
Jetzt muss nur noch der gerade berechnete Wert für t in 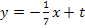eingesetzt werden und wir haben die Sekantengleichung aufgestellt.
Die Gleichung der Sekante lautet: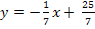 
(Für x und y darf jetzt natürlich nichts eingesetzt werden, sonst läge ja keine Funktionsgleichung mehr vor. Eine Funktion ordnet schließlich jedem x genau ein y zu. Also muss in der Gleichung auch i>x und y vorkommen. Statt y kann natürlich auch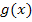 
oder etwas Ähnliches geschrieben werden. Zur Berechnung von t werden zwar die Koordinaten eines Kurvenpunktes für x und y eingesetzt, am Ende der Rechnung beim Aufstellen der Funktionsgleichung der Sekante aber nicht!)
Damit sind wir fertig. Es ist hier nicht verlangt, die Sekante in ein Koordinatensystem zu zeichnen. Das wäre ja auch ganz einfach, da man die Sekante auch mit den beiden bekannten Punkten 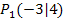und 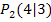zeichnen könnte.
