Herleitung der Tangentensteigung aus der Sekantensteigung mittels des Differenzialquotienten
In der Schule wird jedoch fast ausschließlich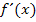 
für die erste Ableitung geschrieben. Erst auf der Universität wird die Schreibweise 
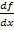für die erste Ableitung wichtig. Falls dir das jetzt noch nichts sagt, ist das nicht schlimm. Es wird später noch ganz ausführlich erklärt. Solltest du später einmal die Schreibweise 
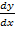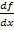bzw. irgendwo sehen, weißt du nun wenigstens, woher das kommt, nämlich von der Formel für die Steigung 
.
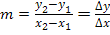Die Formel 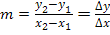brauchst du beispielsweise bei der Berechnung der Sekantensteigung. Eine Sekante ist, wie du sicher weißt, eine Gerade, die eine Funktion 
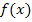schneidet;im Gegensatz zu einer Tangente, die den Funktionsgraphen nur berührt. Später werden wir auch die Gleichung einer Tangente ermitteln. Da wir momentan aber noch nicht besprochen haben, wie sich die Tangentensteigung berechnen lässt, begnügen wir uns erst ´mal mit der wesentlich einfacheren Berechnung der Sekantensteigung. Daraus werden wir später die Tangentensteigung herleiten. Vorweg schauen wir uns aber erst einmal ein Beispiel zur Berechnung einer Sekante an.
Bsp.:
Berechne die Gleichung der Sekante durch die Kurvenpunkte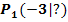 
und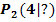 
der Funktion 
!
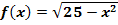Lösung:
Eine Sekante ist logischerweise eine lineare Funktion (Gerade) und hat deshalb allgemein die Gleichung 
. Zuerst muss man die Steigung m berechnen. Dazu verwenden wir die Formel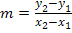 
. Die y-Koordinaten der beiden Punkte 
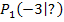und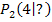 
müssen erst noch ermittelt werden. Man muss nur die jeweilige x-Koordinate in die Funktionsgleichung 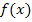einsetzen und schon hat man die y-Koordinate berechnet. 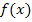ist schließlich nur eine andere Schreibweise für y.
Berechnung der y-Koordinate von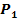 
:
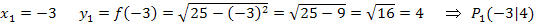
Berechnung der y-Koordinate von 
:
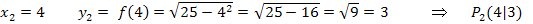
Nun können wir die Sekantensteigung m ausrechnen. Das kannst du sicher auch alleine. Versuche es doch gleich einmal! Dazu musst du ja nur die Koordinaten der beiden Punkte 
und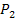 
in die Formel für die Steigung m einsetzen.
Berechnung der Sekantensteigung m:
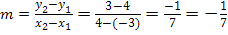
Wir wollen nun ausgehend von diesem konkreten Beispiel einen allgemeinen Ausdruck für die Sekantensteigung herleiten. Überlege dir dazu noch einmal, wie die y-Koordinaten berechnet wurden! Wir haben die x-Koordinaten der beiden Punkte 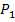und 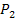, also hier 
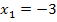bzw. 
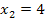, in 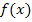eingesetzt. Dies kann man auch in der Form 
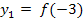und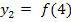 
schreiben.
Mit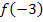 
, sprich:„f von Minus Drei“ , ist somit gemeint, dass man die x-Koordinate x = -3 in die Funktionsgleichung der Funktion 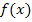einsetzen soll. 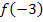ergibt dann die zu x = -3 gehörige y-Koordinate des Punktes auf der Funktion .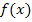
