Herleitung der Tangentensteigung aus der Sekantensteigung mittels des Differenzialquotienten
Allgemein muss das jedoch nicht so sein. Nur bei gleichen x-Koordinaten ergäbe sich ein Problem:Es würde sich eine senkrechte Gerade ergeben. Dies wäre keine Funktion und man könnte auch gar kein Steigungsdreieck einzeichnen. Deshalb müssen die x-Koordinaten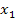 
und 
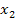der beiden Punkte immer verschieden sein.
Wir kennen also die x-Koordinaten 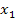und 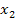. Um die waagrechte rosafarbene Strecke zu ermitteln, muss man von der längeren Strecke 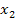die kürzere Strecke 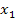abziehen. (Bei 
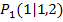und 
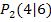heißt das, man muss 4 – 1 rechnen.) Schau dir einfach die entsprechenden Strecken in der Abbildung oben an! Unter der x-Achse sind die entsprechenden Längen 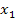und 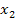zu sehen. Damit müsste dir klar sein, warum die waagrechte rosafarbene Strecke des Steigungsdreiecks mit 
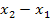berechnet wird.
Bei der Berechnung der senkrechten rosafarbenen Strecke des Steigungsdreiecks gehen wir entsprechend mit den y-Koordinaten vor. Von der längeren Strecke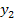 
ziehen wir die kürzere Strecke 
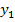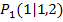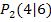ab. (Bei und heißt das, man muss 6 – 1,2 rechnen.)Die Strecken 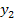und 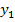kannst du in der Abbildung links neben der y-Achse sehen. Nun müsste dir klar sein, warum die Länge der senkrechten rosafarbenen Strecke des Steigungsdreiecks mit 
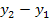berechnet wird.
Die Steigung m erhält man, indem man 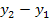durch 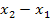dividiert. So kommt man auf die folgende Formel für die Steigung:
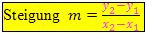
Wie du aus der Physik sicher weißt, kann man für den Unterschied der x-Koordinaten 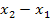auch △x (sprich:„Delta x“) schreiben. Entsprechend kann natürlich auch für den Unterschied der y-Koordinaten 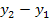auch △y (sprich:„Delta y“) geschrieben werden. Daher gilt für die Steigung m auch:
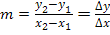
Anmerkung:
In der Mathematik wird an Stelle von △ (Delta) für einen Unterschied auch oft nur d verwendet. Daher kommt die sogenannte Leibniz´sche Schreibweise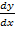 
bzw.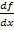 
der ersten Ableitung 
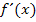– sprich „f Strich von x“ – einer Funktion. Was die erste Ableitung einer Funktion ist, wird weiter unten noch ganz genau erklärt. Für den Moment reicht es, wenn du dir merkst, dass die sogenannte erste Ableitung 
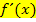die Steigung der Funktion bzw. die Steigung der Tangente an den Graph der Funktion 
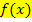in einem beliebigen Kurvenpunkt P 
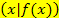beschreibt. Für die Steigung einer Funktion 
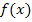, also für die Tangentensteigung, schreibt man anstatt m nun 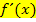oder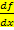 
(sprich:„df nach dx“). Die erste Ableitung 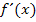entspricht also der Steigung der Kurve 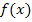, so wie m die Steigung einer Geraden darstellt. Die Leibniz´sche Schreibweise 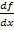ist absolut gleichbedeutend mit .
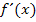