Ausführliche Erklärungen zur faktorisierten Form im 4. Bsp.

Die gesuchte Polynomfunktion fünften Grades hat laut Angabe eine doppelte Nullstelle bei 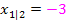und eine dreifache Nullstelle bei .

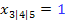Wie kommt man jetzt auf den Ansatz 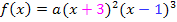für die Polynomfunktion?

Die Exponenten der Klammern erhält man durch die angegeben Vielfachheiten der Nullstellen. Daher steht außerhalb der Klammer bei der doppelten Nullstelle der Exponent 2 und bei der dreifachen Nullstelle der Exponent 3.

Die Zahlen innerhalb der Klammern (hinter dem x) bekommt man, indem man die Vorzeichen der Nullstellen jeweils umdreht.

Warum man die Vorzeichen umdrehen muss?

Allgemein lautet der Ansatz einer Polynomfunktion fünften Grades mit einer doppelten Nullstelle 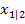und einer dreifachen Nullstelle :

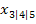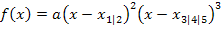
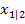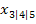In diesem Ansatz steht vor den Nullstellen und jeweils ein Minus. Dieses Minus führt dazu, dass sich die Vorzeichen der Nullstellen jeweils umdrehen.

Mit 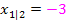und 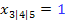ergibt sich:

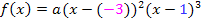
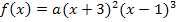
Wenn du zur Kontrolle eine der Nullstellen einsetzt, wirst du feststellen, dass sich dabei für wirklich Null ergibt. Bei einer Nullstelle muss ja der y-Wert gleich Null sein. Setzt man -3 in ein, kommt Null heraus, weil die erste Klammer Null ergibt. Setzt man 1 ein, wird die zweite Klammer gleich Null und somit auch wieder das ganze Produkt gleich Null. Ein Produkt ist schließlich gleich Null, wenn einer der Faktoren gleich Null ist. 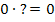bzw.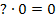

Die Zahlen -3 und +3 heben sich gegenseitig auf: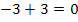

Deshalb muss die erste Klammer 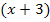lauten, damit Null herauskommt, wenn man für x den Wert -3 einsetzt.

Entsprechend bei der zweiten Klammer. Die Zahlen +1 und -1 heben sich gegenseitig auf: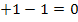

Deshalb muss die zweite Klammer 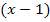lauten, damit Null herauskommt, wenn man für x den Wert 1 einsetzt.

Nun müsste dir eigentlich klar sein, warum man die Vorzeichen der Nullstellen umdrehen muss, um jeweils auf die Zahlen hinter dem x in den Klammern zu kommen. (Mehr dazu bei Faktorisierter Funktionsterm)

---