Funktionsgleichungen mit gegebenen Eigenschaften aufstellen und Funktionen modellieren

Zusammenfassend kann man sagen, dass die Funktionsgleichung 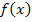immer dann verwendet werden muss, wenn die x-Koordinate und die y-Koordinate eines Kurvenpunktes gegeben sind: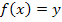

Die erste Ableitung 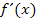wird immer dann verwendet, wenn die Steigung m an einer bestimmten Stelle x bekannt ist: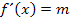

Die zweite Ableitung 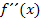wird nur im Zusammenhang mit der Angabe „Wendepunkt“ oder „Terrassenpunkt“ benötigt.

Die dritte Ableitung 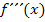braucht man beim Aufstellen von Funktionsgleichungen gar nicht.

Vorsicht:Niemals die erste oder zweite Ableitung mit der y-Koordinate eines angegebenen Punktes kombinieren!

Beispiel:Gegeben ist der Hochpunkt 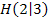einer gesuchten Funktion

Darin stecken die Informationen: 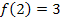und

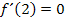
Falsch wäre dagegen: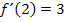

Warum? 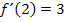bedeutet nämlich, dass der Graph an der Stelle 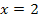die Steigung 3 hat. Das ist aber beim Hochpunkt 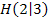sicher nicht der Fall, denn hier verläuft die Tangente schließlich waagrecht. D.h. im Hochpunkt 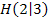ist die Steigung/erste Ableitung gleich 0 und nicht gleich 3. Nur die y-Koordinate ist 3, aber y hat nichts mit der Steigung, also mit der ersten Ableitung zu tun! Daher ist 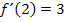hier falsch.

Korrekt ist beim Hochpunkt 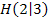dagegen 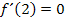. Das drückt wirklich aus, dass bei 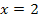die Tangente waagrecht verläuft, also die Steigung/erste Ableitung gleich Null ist. Des Weiteren gilt auch 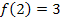, denn dies bedeutet, dass der Kurvenpunkt 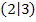auf der Funktion liegt;zur x-Koordinate 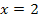gehört der Funktionswert, die y-Koordinate 3. entspricht schließlich y.

Und noch ein kleiner Test, ob du es wirklich verstanden hast:

Welche Information(en) kannst du aus der Angabe „Wendepunkt 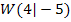“ entnehmen?

Überlege es dir nun erst selbst, bevor du weiter liest!

Aus der Angabe „Wendepunkt 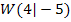“ lassen sich zwei Informationen entnehmen:

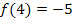und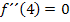

Erläuterung:

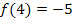bedeutet, dass der Punkt mit den Koordinaten 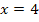und 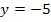auf der Funktion liegt. Der Wendepunkt 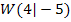hat ja genau diese Koordinaten.

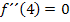bedeutet, dass an der Stelle 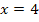die Krümmung/zweite Ableitung gleich Null ist. Im Wendepunkt ist die Krümmung bekanntlich gleich Null, daher werden Wendepunkte ja auch mit 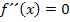berechnet.

Falsch wäre dagegen: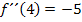

Das würde nämlich bedeuten, dass die Krümmung an der Stelle 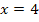den Wert 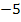hat. Im Wendepunkt muss die Krümmung aber, wie gesagt, gleich Null und nicht 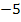sein!

---