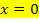Funktionsgleichungen mit gegebenen Eigenschaften aufstellen und Funktionen modellieren
Tabelle Nr.1
| Angabe im Text | Daraus zu entnehmende Information(en) |
Der Graph schneidet die x-Achse an der Stelle 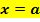 Vergleiche 1. Und 2. Bsp.! Vergleiche 1. Und 2. Bsp.!
Andere Formulierung:Nullstelle bei (Der Buchstabe a steht hier für eine konkret angegebene Zahl.) |
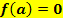 |
Der Graph schneidet die x-Achse an der Stelle 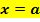 unter dem Winkel unter dem Winkel 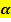
(Der Buchstabe a steht für eine konkrete Zahl und |
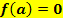
|
Der Graph hat an der Stelle 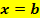 einen Hochpunkt oder Tiefpunkt, d.h. einen Extrempunkt Vergleiche 1. Bsp.! einen Hochpunkt oder Tiefpunkt, d.h. einen Extrempunkt Vergleiche 1. Bsp.!
Andere Formulierung:Waagrechte Tangente bei (Der Buchstabe b steht hier für eine konkret angegebene Zahl.) |
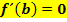 |
Der Graph hat den Hochpunkt 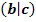 bzw. den Tiefpunkt bzw. den Tiefpunkt 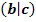 , d.h. den Extrempunkt , d.h. den Extrempunkt 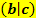
Andere Formulierung:Maximum oder Minimum im Punkt (Die Buchstaben b und c stehen für die Koordinaten des angegebenen Hoch- bzw. Tiefpunktes, d.h. für konkrete Zahlen.) |
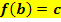
|
Der Graph hat an der Stelle 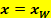 einen Wendepunkt. Vergleiche 1. Bsp.! einen Wendepunkt. Vergleiche 1. Bsp.!
Andere Formulierung:Flachpunkt bei oder „der Graph verläuft an der Stelle (Die Bezeichnung |
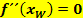 |
Der Graph hat den Wendepunkt 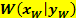 . Vergleiche 3. Bsp.! . Vergleiche 3. Bsp.!
Andere Formulierung: Flachpunkt (Die Bezeichnungen |
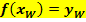
|
Der Graph hat an der Stelle 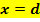 einen Terrassenpunkt. einen Terrassenpunkt.
Andere Formulierung:Terrassenpunkt (Mit dem Buchstaben d ist die angegebene x-Koordinate des Terrassenpunktes gemeint.) |
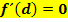
|
Der Graph hat den Terrassenpunkt 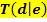 . .
Vergleiche 3. Bsp.! (Mit den Buchstaben d und e sind die Koordinaten des angegebenen Terrassenpunktes gemeint.) |
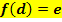
|
Die Tangente im Kurvenpunkt 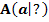 verläuft parallel zur Gerade verläuft parallel zur Gerade 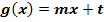
Andere Formulierung:Die Funktion hat an der Stelle (Mit dem Buchstaben a ist die x-Koordinate des Kurvenpunktes gemeint, wo die Steigung den gegebenen Wert m hat. a und m sind also konkrete Zahlen. Auch t stellt eine konkrete Zahl dar. t steht für den y-Achsenabschnitt der angegeben Gerade, also der Parallele zur Tangente. t ist eine unnötige Angabe;man braucht t hier gar nicht.) |
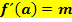 |
Der Graph hat den Wendepunkt 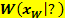 mit der Wendetangente mit der Wendetangente 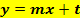 . .
Achtung: Die y-Koordinate (Mit |
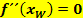
mit . |
Der gesuchte Graph soll im Punkt 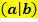 ohne Knick, also weich in eine Gerade mit der Steigung m übergehen. Vergleiche Einführungsbeispiel! ohne Knick, also weich in eine Gerade mit der Steigung m übergehen. Vergleiche Einführungsbeispiel!
Andere Formulierung:Die Funktion hat im Punkt (Mit a, b und m sind konkrete, angegebene Zahlen gemeint.) |
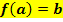
|
Gegeben ist eine Funktion 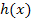 mit ihrer Funktionsgleichung. Gesucht ist eine Funktion mit ihrer Funktionsgleichung. Gesucht ist eine Funktion  . Die beiden Funktionen . Die beiden Funktionen 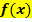 und und 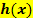 sollen sich an der Stelle sollen sich an der Stelle 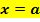 berühren. berühren.
Hinweis: Zwei Funktionen, die sich bei |
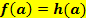
|
| Die Funktion ist achsensymmetrisch zur y-Achse. | Es kommen nur gerade Potenzen von x im Funktionsterm vor. Vergleiche Tabelle Nr. 2! |
| Die Funktion ist punktsymmetrisch zum Ursprung. | Es kommen nur ungerade Potenzen von x im Funktionsterm vor. Vergleiche Tabelle Nr. 2! |
Im Schnittpunkt mit der y-Achse hat der Graph die Tangente mit der Gleichung 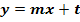
Andere Formulierung: Der Graph schneidet die y-Achse bei t und hat dort die Steigung m. Oder:Der Graph schneidet die y-Achse bei t und die Tangente ist parallel zur Geraden (Mit m und t sind konkrete Zahlen gemeint. Dabei stellt m die Steigung der Tangente dar und t den y-Achsenabschnitt. Auch mit |
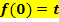
Erklärung: Jeder Punkt, der auf der y-Achse liegt, hat die x-Koordinate
Daher gilt: Die Steigung im Schnittpunkt mit der y-Achse, also an der Stelle
Merke: Die Angabe „Schnittpunkt mit der y-Achse“ entspricht „an der Stelle |

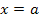
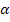 steht für einen konkret angegebenen Winkel.)
steht für einen konkret angegebenen Winkel.)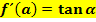
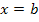
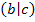
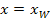
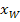 steht hier für die angegebene x-Koordinate des Wendepunktes, also für eine konkrete Zahl.)
steht hier für die angegebene x-Koordinate des Wendepunktes, also für eine konkrete Zahl.)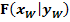
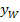 stehen für die angegebenen Koordinaten des Wendepunktes bzw. Flachpunktes, also für konkrete Zahlen.)
stehen für die angegebenen Koordinaten des Wendepunktes bzw. Flachpunktes, also für konkrete Zahlen.)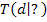
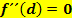
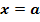 die Steigung m.
die Steigung m.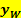
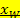
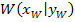 bekannt. Vergleiche 2. Bsp.!
bekannt. Vergleiche 2. Bsp.!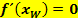
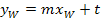 , d.h. du musst die gegebende x-Koordinate
, d.h. du musst die gegebende x-Koordinate 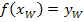 .
.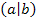 die Steigung m.
die Steigung m.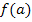 und
und 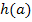 , als auch die gleichen Steigungen
, als auch die gleichen Steigungen 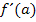 und
und 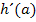 . Vergleiche 6. Bsp.!
. Vergleiche 6. Bsp.!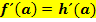
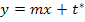 .
.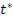 ist eine konkrete Zahl gemeint.
ist eine konkrete Zahl gemeint. 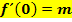
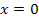 , weil man auf der x-Achse weder nach links noch nach rechts geht. Daher weißman, dass die x-Koordinate des Schnittpunkts mit der y-Achse
, weil man auf der x-Achse weder nach links noch nach rechts geht. Daher weißman, dass die x-Koordinate des Schnittpunkts mit der y-Achse  .) So ergibt sich:
.) So ergibt sich: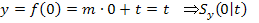
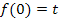
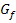 ist die erste Ableitung an dieser Stelle, in diesem Fall beim Schnittpunkt mit der y-Achse, also bei
ist die erste Ableitung an dieser Stelle, in diesem Fall beim Schnittpunkt mit der y-Achse, also bei