Funktionsgleichungen mit gegebenen Eigenschaften aufstellen und Funktionen modellieren
TIPP:Wenn in einer Aufgabe zum Beispiel steht, dass die gesuchte Funktion  den Hochpunkt H(2|4) und den Wendepunkt W(-3|1) besitzt, sind darin vier Informationen über die Funktion
den Hochpunkt H(2|4) und den Wendepunkt W(-3|1) besitzt, sind darin vier Informationen über die Funktion  enthalten, nicht nur zwei! Beachte also beim Heraussuchen der Informationen aus der Angabe, dass in Formulierungen der Art „Hochpunkt H(2|4)“ oder „Wendepunkt W(-3|1)“ jeweils gleich zwei Informationen enthalten sind, nämlich einmal die Koordinaten des Kurvenpunkts H bzw. W und dann noch zusätzlich die zweite Information, dass es sich dabei um einen Hochpunkt bzw. Wendepunkt handelt, also dass die erste bzw. zweite Ableitung an dieser Stelle gleich Null ist.
enthalten, nicht nur zwei! Beachte also beim Heraussuchen der Informationen aus der Angabe, dass in Formulierungen der Art „Hochpunkt H(2|4)“ oder „Wendepunkt W(-3|1)“ jeweils gleich zwei Informationen enthalten sind, nämlich einmal die Koordinaten des Kurvenpunkts H bzw. W und dann noch zusätzlich die zweite Information, dass es sich dabei um einen Hochpunkt bzw. Wendepunkt handelt, also dass die erste bzw. zweite Ableitung an dieser Stelle gleich Null ist.
Aus der Angabe „Hochpunkt H(2|4)“ ergeben sich beispielsweise folgende zwei Informationen:
1. Information ![]() er Kurvenpunkt H hat die Koordinaten
er Kurvenpunkt H hat die Koordinaten 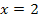 und
und 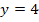 . Da
. Da 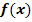 nur eine andere Schreibweise für y ist, gilt:
nur eine andere Schreibweise für y ist, gilt: 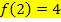
2. Information:An der Stelle 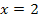 ist ein Hochpunkt, also ist die Steigung/erste Ableitung dort gleich Null:
ist ein Hochpunkt, also ist die Steigung/erste Ableitung dort gleich Null: 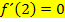
Aus der Angabe „Wendepunkt W(-3|1)“ ergeben sich beispielsweise die folgenden beiden weiteren Informationen:
3. Information ![]() er Kurvenpunkt W hat die Koordinaten
er Kurvenpunkt W hat die Koordinaten 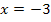 und
und 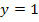 . Da
. Da 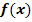 nur eine andere Schreibweise für y ist, gilt:
nur eine andere Schreibweise für y ist, gilt: 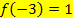
4. Information:An der Stelle 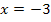 ist ein Wendepunkt, also ist die Krümmung/zweite Ableitung dort gleich Null:
ist ein Wendepunkt, also ist die Krümmung/zweite Ableitung dort gleich Null: 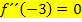
Steht in der Angabe beispielsweise, dass die gesuchte Funktion  den Terrassenpunkt T(1,5|2) hat, ergeben sich sogar drei Informationen über
den Terrassenpunkt T(1,5|2) hat, ergeben sich sogar drei Informationen über  .
.
1. Information ![]() er Kurvenpunkt T hat die Koordinaten
er Kurvenpunkt T hat die Koordinaten 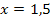 und
und 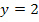 . Da
. Da 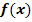 nur eine andere Schreibweise für y ist, gilt:
nur eine andere Schreibweise für y ist, gilt: 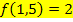
2. Information:An der Stelle 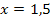 ist ein Terrassenpunkt, also ein Punkt mit waagrechter Tangente und ist die Steigung/erste Ableitung dort gleich Null:
ist ein Terrassenpunkt, also ein Punkt mit waagrechter Tangente und ist die Steigung/erste Ableitung dort gleich Null: 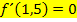
3. Information:An der Stelle 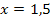 ist ein Terrassenpunkt, d.h. ein Wendepunkt, also ist die Krümmung/zweite Ableitung dort gleich Null:
ist ein Terrassenpunkt, d.h. ein Wendepunkt, also ist die Krümmung/zweite Ableitung dort gleich Null: 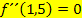
Wenn in der Angabe zum Beispiel „an der Stelle 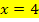 verläuft die Tangente an den Graph
verläuft die Tangente an den Graph 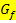 parallel zur Gerade
parallel zur Gerade 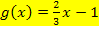 “ steht, kannst du die Tangentensteigung/erste Ableitung an dieser Stelle entnehmen. Da parallele Geraden die gleiche Steigung besitzen, muss die Tangente die gleiche Steigung wie die Gerade
“ steht, kannst du die Tangentensteigung/erste Ableitung an dieser Stelle entnehmen. Da parallele Geraden die gleiche Steigung besitzen, muss die Tangente die gleiche Steigung wie die Gerade 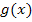 haben, also in diesem Beispiel die Steigung
haben, also in diesem Beispiel die Steigung 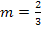 . Deshalb gilt:
. Deshalb gilt: 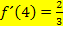
Damit es dir leichter fällt, die Informationen aus der jeweiligen Angabe zu entnehmen, sind die häufigsten Formulierungen mit der zugehörigen mathematischen Schreibweise der Information über die Funktion  in der Tabelle Nr. 1 zusammengefasst.
in der Tabelle Nr. 1 zusammengefasst.

