Funktionsgleichungen mit gegebenen Eigenschaften aufstellen und Funktionen modellieren

Lösung des Gleichungssystems:

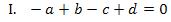
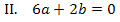
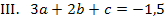
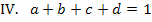
Im ersten Schritt ziehen wir Gleichung I. von Gleichung IV. ab. Dadurch fällt nämlich die Unbekannte d heraus, die in den anderen Gleichungen auch nicht vorkommt. (Man könnte genauso gut von  Gleichung IV. die Gleichung I. abziehen. Hauptsache d fällt weg.) Die aus IV. minus I. entstehende Gleichung nennen wir V.

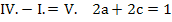
p>Nun haben wir mit V. eine Gleichung vor uns, die nur die Unbekannten a und c enthält. Um die beiden Unbekannten a und c berechnen zu können, benötigen wir eine zweite Gleichung, die nur a und c enthält. Wir erhalten eine derartige Gleichung, indem wir von Gleichung III. die Gleichung II. abziehen. Dann fällt nämlich b heraus. Die aus III. minus II. entstehende Gleichung bezeichnen wir mit VI.

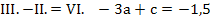
Die beiden Gleichungen V. und VI. enthalten nur noch die beiden Unbekannten a und c, die sich jetzt leicht ermitteln lassen. (Zwei Gleichungen für zwei Unbekannte.)

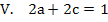
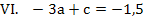
Ob man nun wieder mit dem Additionsverfahren oder lieber mit dem Einsetzungsverfahren arbeiten will, bleibt jedem selbst überlassen. Wir verwenden hier jetzt das Einsetzungsverfahren, weil sich VI. so schön nach c auflösen lässt. Wir lösen also Gleichung VI. nach c auf und setzen das Ergebnis für c in Gleichung V. ein.

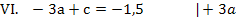
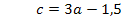
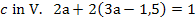
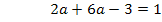
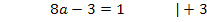
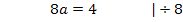
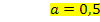
Den soeben berechneten Wert setzen wir nun für a in die nach c aufgelöste Form von Gleichung VI. ein, also in 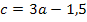. So bekommen wir c heraus.

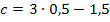
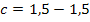
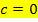
Um die Unbekannte b zu erhalten, setzen wir die ermittelten Werte a = 0,5 und c = 0 in Gleichung III. ein.

Hier noch einmal Gleichung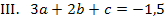

a und c in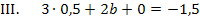

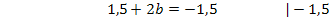
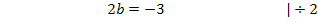
Jetzt wissen wir: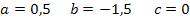

Es fehlt nur noch die Unbekannte d. Wir erhalten sie, indem wir die berechneten Werte von a, b und c entweder in Gleichung 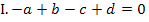oder in 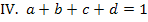einsetzen. Wir nehmen hier IV.

a, b und c in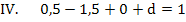

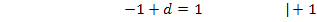
Nun haben wir alle vier Unbekannten ermittelt: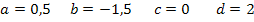

Wir müssen nur noch alles in den allgemeinen Ansatz 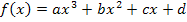einsetzen.

Die gesuchte Funktion lautet: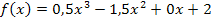

Oder einfacher geschrieben: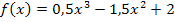

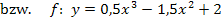
Damit ist die Aufgabe gelöst. In der folgenden Abbildung kannst du den Graph der Funktion 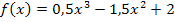sehen.

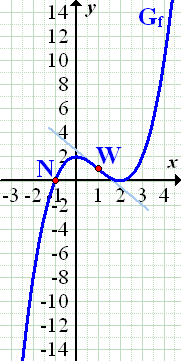
Abb.:Graph 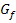der Funktion 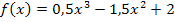mit der gegebenen Nullstelle 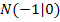und der Wendetangente 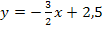in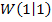

Die gesuchte Funktion sollte die x-Achse bei x = -1 schneiden und bei x = 1 einen Wendepunkt mit der Wendetangente 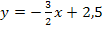besitzen. Offensichtlich erfüllt die ermittelte Funktion 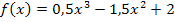die Bedingungen. Das Ergebnis ist daher zwangsläufig korrekt.

Nun müsste dir das Prinzip solcher Aufgaben eigentlich schon klar sein. Versuche die nächste Aufgabe erst alleine zu lösen, bevor du dir die Lösung anschaust!

---