Funktionsgleichungen mit gegebenen Eigenschaften aufstellen und Funktionen modellieren
Daher lautet unser Ansatz:
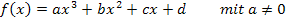
Wir bilden die ersten beiden Ableitungen. Die zweite Ableitung brauchen wir wegen der Angabe des Wendepunkts. (Nur wenn in der Aufgabe ein Flachpunkt, Wendepunkt oder Terrassenpunkt gegeben ist, oder zumindest seine x-Koordinate, muss die zweite Ableitung gebildet werden.)
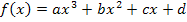
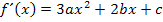
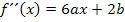
Wir müssen hier die vier Unbekannten a, b, c und d berechnen. Daher brauchen wir vier Gleichungen, also vier verschiedenen Informationen.
1. Information 
er Graph der Funktion schneidet die x-Achse bei 
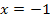, d.h. bei 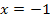hat er eine Nullstelle. Bekanntlich berechnet man Nullstellen durch 
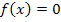. Daher gilt hier:
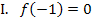
Zweite Information:Bei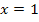 
hat der Graph einen Wendepunkt. Wendepunkte berechnet man bekanntlich mit dem Ansatz 
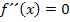, da sich im Wendepunkt das Krümmungsverhalten, also das Vorzeichen der zweiten Ableitung ändert. Die zweite Ableitung entspricht schließlich der Krümmung des Graphen. Daher gilt:
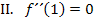
Jetzt fehlen noch zwei weitere Informationen. Du kannst dir schon denken, dass sie in der Wendetangente versteckt sind.
Dritte Information ie Wendetangente im Wendepunkt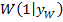 
hat die Gleichung 
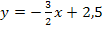, sie hat also die Steigung 
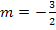. Die Wendetangente berührt den Funktionsgraphen genau im Wendepunkt 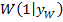. Berühren sich zwei Funktionen in einem bestimmten Punkt, haben sie dort die gleiche Steigung. Die Funktion hat im Wendepunkt genau die Steigung der Wendetangente. Die Funktion 
hat deshalb an der Stelle 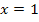die Steigung 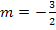. Die Steigung einer Funktion wird durch ihre erste Ableitung beschrieben. Somit gilt:
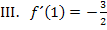
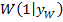Vierte Information er Wendepunkt liegt nicht nur auf dem Funktionsgraphen von , sondern auch auf der zugehörigen Wendetangente 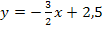. Daher kann man die y-Koordinate 
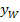des Wendepunktes berechnen, indem man seine x-Koordinate in die Wendetangente einsetzt.
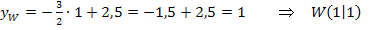
Dass die x-Koordinate mit der y-Koordinate des Wendepunktes übereinstimmt, ist reiner Zufall. Auf jeden Fall kennen wir nun beide Koordinaten des Wendepunktes. Wegen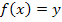 
ergibt sich die letzte Information:
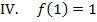
Nun kennen wir die vier nötigen Informationen. Wir müssen jetzt die zugehörigen Gleichungen aufstellen.
Hier noch einmal die Funktionsgleichung und ihre ersten zwei Ableitungen in der allgemeinen Form:
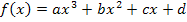
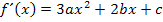
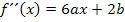
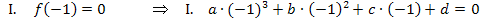
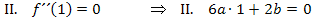
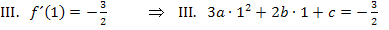
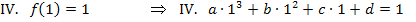
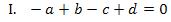
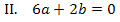
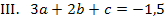
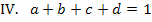
Jetzt müssen wir das Gleichungssystem lösen. Wenn man dabei geschickt mit dem Additionsverfahren arbeitet, kommt man relativ schnell zur Lösung. Das Einsetzungsverfahren ist zwar auch möglich, dauert aber wesentlich länger. Daher ist davon dringend abzuraten! Am besten man kombiniert beide Verfahren geschickt miteinander. Versuche doch gleich mal alleine das Gleichungssystem zu lösen und vergleiche dann erst mit dem im Folgenden gezeigten Rechenweg.
