Funktionsgleichungen mit gegebenen Eigenschaften aufstellen und Funktionen modellieren
(Siehe auch:Gleichungssysteme:Zwei Gleichungen für zwei Unbekannte und Gleichungssysteme:Drei Gleichungen für drei Unbekannte)
Zu deiner Kontrolle, hier natürlich der komplette Rechenweg:
c und d in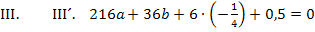 
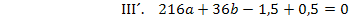
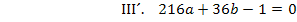
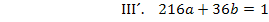
c in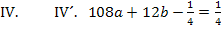 
c in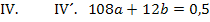 
Nun ist folgendes Gleichungssystem zu lösen:
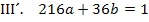
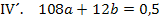
Wir verwenden hier das Additionsverfahren. Damit sich nachher bei der Addition der beiden Gleichungen die Unbekannte b heraushebt, muss vorher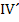 
mit dem Faktor -3 multipliziert werden.
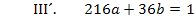
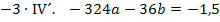
Durch Addition der beiden Gleichungen ergibt sich:
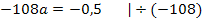
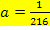
Nun kann die letzte Unbekannte b leicht berechnet werden, indem man a in III´oder IV´einsetzt. Wir setzen hier in III´ein.
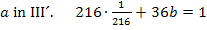
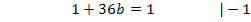
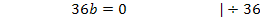
Jetzt haben wir alle vier Unbekannten ermittelt: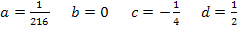 
Wir müssen sie nur noch in den allgemeinen Ansatz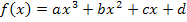 
einsetzen. So ergibt sich die gesuchte Funktion:
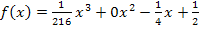
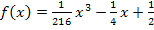
Damit ist die Aufgabe gelöst. Die Funktion 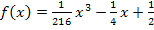mit 
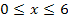verbindet die beiden gegebenen Geraden in einem weichen Bogen.
Nicht alle Aufgaben dieses Aufgabentyps sind Anwendungsaufgaben. Oft sind einfach bestimmte Punkte, wie Extrema oder Wendepunkte der gesuchten Funktion gegeben. Schauen wir uns gleich ein paar typische Beispiele dafür an.
1. Bsp.:
Der Graph einer Funktion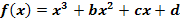 
schneidet die x-Achse bei 
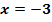, hat an der Stelle 
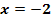einen Hochpunkt und bei 
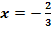einen Wendepunkt. Bestimme die Gleichung von 
!
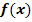Lösung:
Wir bilden vorweg die erste und zweite Ableitung von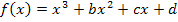 
. Die Konstanten b und c bleiben beim ersten Ableiten stehen, da es sich um multiplikative Konstanten (Zahlen, die mit x oder einer Potenz von x multipliziert werden) handelt. Die Konstante d fällt dagegen beim Bilden der ersten Ableitung weg, da es sich bei d um eine additive Konstante (Zahl ohne x, die addiert wird) handelt und additive Konstanten beim Ableiten bekanntlich Null ergeben und somit wegfallen. Das Gleiche gilt dann beim Bilden der zweiten Ableitung für c. (Näheres bei Einfache Ableitungsregeln)
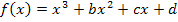
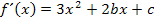
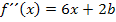
Nun suchen wir die relevanten Informationen aus der Angabe heraus. Wir müssen drei Gleichungen aufstellen, weil wir drei Unbekannte berechnen müssen. Also brauchen wir drei Informationen über die Funktion.
Erste Information 
er Graph der Funktion schneidet die x-Achse bei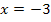 
, d.h. bei 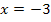ist eine Nullstelle. Bekanntlich berechnet man Nullstellen durch 
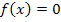. Daher gilt hier:
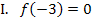
Zweite Information:Bei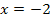 
liegt ein Hochpunkt, also ein Extremum der Funktion.
