Funktionsgleichungen mit gegebenen Eigenschaften aufstellen und Funktionen modellieren

Um vier Unbekannte zu berechnen, braucht man vier Gleichungen. Um auf diese Gleichungen zu kommen, benötigen wir vier Informationen über die Funktion .

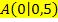1. Information er Punkt liegt auf der gesuchten Funktion .

2. Information:An der Stelle 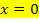muss die Funktion die gleiche Steigung haben wie die linke, d.h. fallende Gerade, also die Steigung .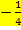

Hinweis:Nur wenn die gesuchte Funktion im Punkt 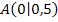die gleiche Steigung hat wie die fallende Gerade, geht die Funktion weich, also ohne Knick in diese Gerade über.

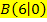3. Information er Punkt liegt ebenfalls auf der Funktion .

4. Information:An der Stelle 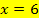muss die Funktion die gleiche Steigung haben wie die rechte, d.h. steigende Gerade, also die Steigung .

Hinweis:Damit im Punkt 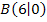weich (ohne Knick) in die rechte Gerade übergeht, muss dort die gleiche Steigung wie diese Gerade haben, also die Steigung .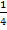

Nun übersetzen wir diese Informationen in eine mathematische Schreibweise.

Zur Erinnerung:

Liegt ein Punkt 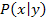auf einer Funktion , dann gilt: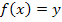

Hat eine Funktion an der Stelle x die Steigung m, dann gilt: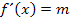

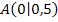
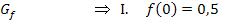
Bei 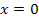ist

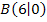
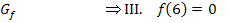
Bei 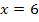ist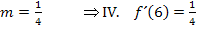

Wir brauchen also die erste Ableitung 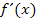, um die Gleichungen II. und IV. aufstellen zu können. Deshalb leiten wir erst einmal die Funktion 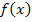in ihrer allgemeinen Form ab. (Näheres dazu bei Einfache Ableitungsregeln)

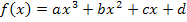
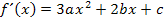
Nun lassen sich die vier benötigten Gleichungen aufstellen:

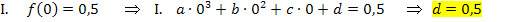
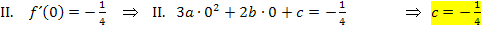
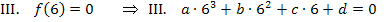
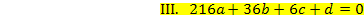
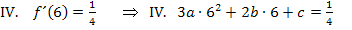
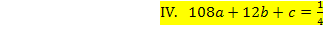
Dir ist nicht klar, wie man auf die einzelnen Gleichungen kommt? Ok, dann noch einmal ganz langsam. Die Gleichung I. erhält man aus 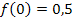. D.h. man soll in für x die Zahl 0 einsetzen und dies gleich 0,5 setzen. Dabei fallen erfreulicherweise die Unbekannten a, b und c heraus. Es ergibt sich direkt 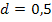. Die Gleichung II. ergibt sich aus 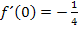, d.h. man soll in 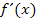für x die Zahl 0 einsetzen und das gleich 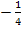setzen. Die Gleichung III. ergibt sich entsprechend aus 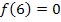, d.h. man soll in für x die Zahl 6 einsetzen und dies gleich 0 setzen. Die Gleichung IV. ergibt sich aus 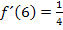, d.h. man soll in 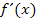für x die Zahl 6 einsetzen und das gleich 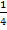setzen.

Merke:

Wenn du die Koordinaten 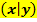eines Kurvenpunktes gegeben hast, immer in die Funktionsgleichung 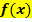einsetzen! Es gilt schließlich: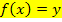

Wenn du die Steigung m an einer bestimmten Stelle x gegeben hast, immer mit der ersten Ableitung 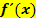arbeiten! Es gilt schließlich: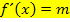

Versuche doch ab jetzt alleine weiter zu rechnen. Du brauchst nur c und d in III. und IV. einzusetzen und dann entweder mit dem Einsetzungs- oder Additionsverfahren das entstehende Gleichungssystem mit zwei Gleichungen und den zwei Unbekannten a und b zu lösen.

---