Funktionsgleichungen mit gegebenen Eigenschaften aufstellen und Funktionen modellieren

Generell sagt man, dass sich zwei Funktionen berühren, wenn sie an einer bestimmten Stelle einen gemeinsamen Punkt und auch die gleiche Steigung an dieser Stelle besitzen. Setzt man zwei Funktionen gleich und es ergibt sich eine doppelte Lösung, so weißman direkt, dass sich die beiden Funktionsgraphen an dieser Stelle berühren. (Eine einfache Lösung entspricht dagegen einem Schnittpunkt.)

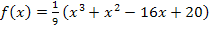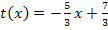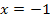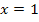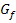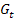Du kannst das an Hand der Funktion und der Tangente aus dem 6. Bsp. nachrechnen. Berechne die x-Koordinaten der gemeinsamen Punkte und nachher jeweils die Steigungen an diesen Stellen. Setze dazu die beiden Funktionen gleich und löse nach x auf. Du wirst eine doppelte Lösung bei (Berührpunkt) und eine einfache Lösung bei (Schnittpunkt) erhalten. Die Steigungen von und bei 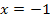sind beide gleich; 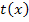ist schließlich die Tangente an 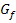bei 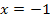. Die Steigungen an der Stelle 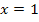sind dagegen unterschiedlich;hier schneiden sich 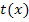und .

Was du an diesem Beispiel lernen solltest: Wenn in einer Aufgabe davon die Rede ist, dass sich zwei Funktionen an einer bestimmten Stelle berühren, darf man keinesfalls vergessen, dass auch die Steigungen, d.h. die ersten Ableitungen, an dieser Stelle jeweils gleich sind, nicht nur die Funktionswerte.

Das soll uns hier an Beispielen genügen. In deinem Mathe-Schulbuch findest du sicher genug weitere Aufgaben dieses Typs zum Üben.

---