Funktionsgleichungen mit gegebenen Eigenschaften aufstellen und Funktionen modellieren
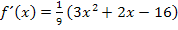
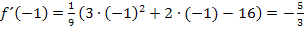
An Stelle von 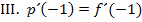 kann man daher auch
kann man daher auch 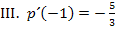 schreiben.
schreiben.
Hinweis:
Würden sich die beiden Funktionen dagegen nur schneiden, aber nicht berühren, läge zwar der Schnittpunkt auf beiden Funktionen, d.h. die Funktionswerte wären an dieser Stelle gleich, aber die Funktionen hätten verschiedene Tangenten. Die Tangentensteigungen wären dann unterschiedlich und somit die ersten Ableitungen an dieser Stelle nicht gleich.
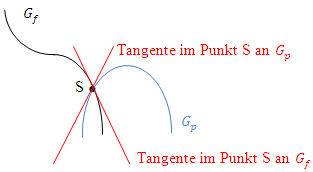
Abb. 2:Zwei Funktionen, die sich im Punkt S schneiden, mit den zugehörigen Tangenten
Jetzt fassen wir noch einmal alles übersichtlich zusammen, was wir inzwischen über die Parabel 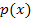 wissen:
wissen:
Allgemeiner Ansatz: 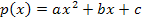
Erste Ableitung: 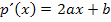
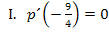
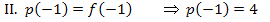
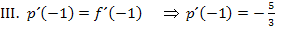
Ab jetzt dürfte es kein Problem mehr für dich sein, die Aufgabe zu lösen. Stelle die drei benötigten Gleichungen auf und berechne die Unbekannten a, b und c alleine, ohne vorher die folgende Lösung anzuschauen!
Zu deiner Kontrolle, hier die komplette Lösung:
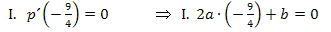
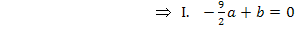
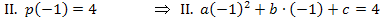
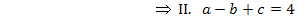
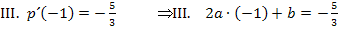
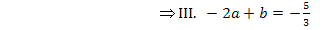
Wir verwenden hier das Additionsverfahren. (Du kannst natürlich auch mit dem Einsetzungsverfahren arbeiten, wenn dir das lieber ist.) Wir subtrahieren III. von I., um b zu eliminieren.
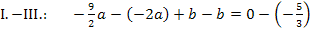
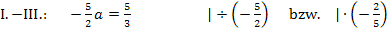

Wir berechnen b, indem wir den soeben berechneten Wert in I. für a einsetzen. (Man kann natürlich auch in III. einsetzen.)
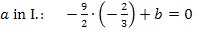
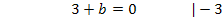

Die verbleibende Unbekannte c berechnen wir durch Einsetzen von a und b in II.
Hier noch einmal 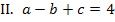
a und b in II.: 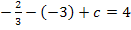
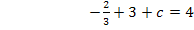
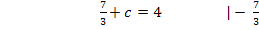

Nun kennen wir alle Koeffizienten: 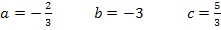
Wir müssen sie nur noch in den allgemeinen Ansatz 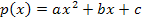 einsetzen und schon haben wir die Gleichung der Parabel ermittelt. Die Parabelgleichung lautet:
einsetzen und schon haben wir die Gleichung der Parabel ermittelt. Die Parabelgleichung lautet:
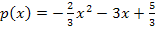
Damit ist die Aufgabe gelöst. In der folgenden Abbildung kannst du die Graphen der Funktionen 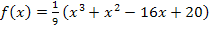 und
und 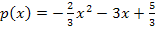 sehen. Außerdem ist ihre gemeinsame Tangente
sehen. Außerdem ist ihre gemeinsame Tangente 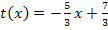 im Punkt
im Punkt 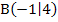 eingezeichnet.
eingezeichnet.
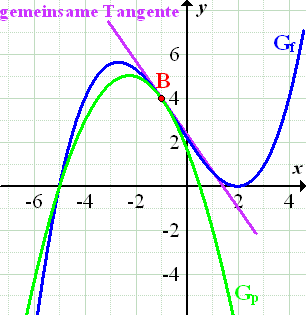
Abb.: Graphen der Funktionen 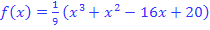 und und 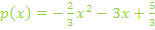 mit gemeinsamer Tangente mit gemeinsamer Tangente 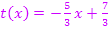 an der Stelle an der Stelle 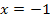 |
Wundere dich nicht darüber, dass die Tangente an der Stelle 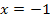 an die beiden Graphen
an die beiden Graphen  und
und  den Graph
den Graph 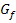 bei
bei 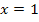 schneidet! Natürlich hast du prinzipiell Recht, wenn du denkst, dass eine Tangente den Graph nur berühren, aber nicht schneiden darf. Doch gilt das nur an einer bestimmten Stelle und der näheren Umgebung dieser Stelle.
schneidet! Natürlich hast du prinzipiell Recht, wenn du denkst, dass eine Tangente den Graph nur berühren, aber nicht schneiden darf. Doch gilt das nur an einer bestimmten Stelle und der näheren Umgebung dieser Stelle.
Die Gerade 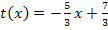 ist an der Stelle
ist an der Stelle 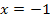 wirklich Tangente an
wirklich Tangente an 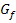 (und an
(und an 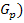 . Sie berührt
. Sie berührt 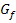 bei
bei 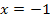 , schneidet
, schneidet 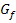 aber auch noch an der Stelle
aber auch noch an der Stelle 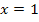 .
.
Merke:Eine Tangente berührt den zugehörigen Funktionsgraph an einer bestimmten Stelle, kann ihn aber etwas weiter entfernt auch noch schneiden!

