Funktionsgleichungen mit gegebenen Eigenschaften aufstellen und Funktionen modellieren

6. Bsp.:Aus Abschlussprüfung FOS 2011 AI /3.1

Gesucht ist die Gleichung einer Parabel 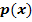, die bei 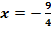ihren Scheitel hat. Die Parabel berührt bei 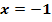den Graph der Funktion .

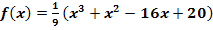Lösung:

Hier ist eine Parabel 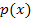gesucht, also eine quadratische Funktion.

Allgemeiner Ansatz: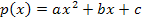

Erste Ableitung: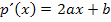

Um die drei Unbekannten a, b und c zu erhalten, brauchen wir drei Gleichungen, also drei Informationen. Die erste Information steckt in der Angabe der x-Koordinate des Scheitels. Der Scheitel liegt bei 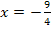. Der Scheitel ist nichts anderes als ein Extremum, daher liegt die Tangente an der Stelle 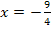waagrecht. Ihre Steigung ist an dieser Stelle somit gleich Null. Deshalb ist die erste Ableitung  bei 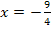gleich Null. So ergibt sich die erste Information:

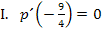
Die zweite und dritte Information sind nicht so leicht zu finden. Laut Angabe berührt die Parabel 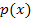die Funktion 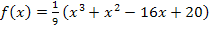an der Stelle 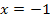. In der Formulierung „berührt“ sind folgende zwei Informationen enthalten:

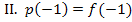
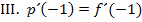
Erläuterung:

Wenn sich die beiden Funktionen 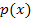und an der Stelle 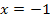berühren, haben sie dort einen gemeinsamen Punkt und auch die gleiche Tangente. Daher sind einerseits die Funktionswerte 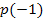und 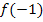gleich, aber auch die Tangentensteigungen 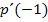und .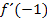

Wenn dir das nicht klar ist, betrachte die unten folgende Skizze! (Abb. 1) Daran kannst du erkennen, dass der Berührpunkt auf beiden Funktionen liegt und, dass beide Funktionen im Berührpunkt die gleiche Tangente haben. Weil der Berührpunkt B auf den beiden Funktionen 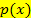und 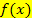liegt, sind die Funktionswerte 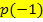und 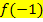gleich und es gilt: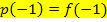

Die Gleichung von ist gegeben, so dass sich 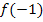leicht berechnen lässt. 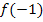ergibt die y-Koordinate 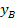des Berührpunktes B. Nach der Berechnung von 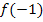kennt man die Koordinaten des Berührpunktes 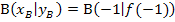, der natürlich auch auf der Parabel liegt. Am besten rechnet man 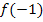vorweg aus.

Hier noch einmal die Funktionsgleichung von : 

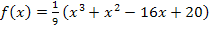
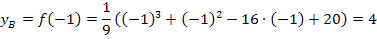
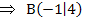
Weil der Berührpunkt 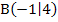auch auf der Parabel 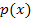liegt, kann man auch schreiben:

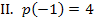
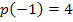ist praktisch das Selbe wie 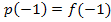, nur dass 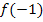schon ausgerechnet ist.

Warum gilt aber auch 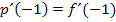? Die gegebene Funktion 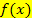und die gesuchte Parabel 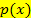haben an der Stelle 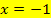die gleiche Tangente;schließlich berühren sie sich dort. Die Tangentensteigung/erste Ableitung muss deshalb an dieser Stelle ebenfalls gleich sein, nicht nur die Funktionswerte. Deshalb gilt: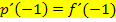

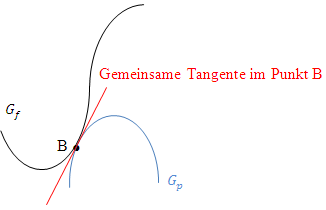
Abb. 1:Zwei Funktionen, die sich im Punkt B berühren, mit zugehöriger Tangente

Da die Funktionsgleichung 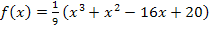bekannt ist, lässt sich die Ableitungsfunktion 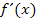und die Ableitung 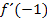, also die Tangentensteigung an der Stelle 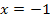leicht ausrechnen.

---