Funktionsgleichungen mit gegebenen Eigenschaften aufstellen und Funktionen modellieren
Aus Gleichung II. lässt sich d direkt ermitteln:
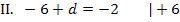
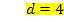
Wir müssen nur noch den soeben berechneten Wert für d in I. einsetzen. Dann lässt sich die letzte Unbekannte e ausrechnen.
d in I.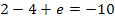 
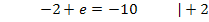
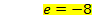
Damit haben wir alle fünf Unbekannten ermittelt:
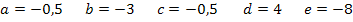
Wir setzten diese Werte in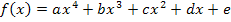 
ein.
Die gesuchte Funktion lautet: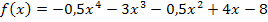 
2. Methode:Nur für Schüler, die bereits gelernt haben Polynomfunktionen zu integrieren!
Um von der zweiten Ableitung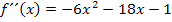 
zur Funktion 
zu kommen, muss zweimal integriert werden. Integrieren ist bekanntlich das Gegenteil des Ableitens. Man integriert Funktionen der Form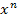 
, indem man zum Exponenten die Zahl 1 dazu zählt und außerdem durch diese Zahl dividiert:
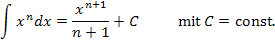
Genaueres dazu im Kapitel Einführung in die Integralrechnung.
Dabei lässt sich die Konstante C bei der Integration nicht direkt ermitteln.
Wenn wir die zweite Ableitung 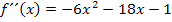einmal integrieren, erhalten wir die erste Ableitung – bis auf die Konstante C.
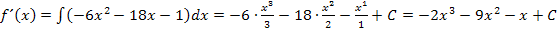
Wir integrieren noch ein weiteres Mal und kommen so zu einem Ansatz für . Allerdings darfst du dabei nicht vergessen, dass noch eine zweite Konstante eingeführt werden muss. Wir nennen diese zweite noch unbekannte Konstante hier D. Sowohl C als auch D können erst später mit Hilfe der anderen Angaben über die Funktion berechnet werden.
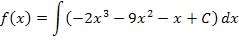
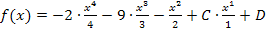
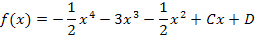
Oder, wenn du lieber mit Kommazahlen (Dezimalbrüchen) rechnest:
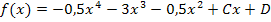
Jetzt müssen aber noch die Konstanten C und D berechnet werden. Dazu braucht man die restlichen Angaben:
Der Graph enthält den Punkt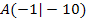 
, so dass gilt: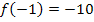 
Außerdem verläuft die Tangente im Punkt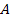 
parallel zur Gerade 
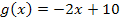. Da die Tangente parallel zu der Gerade 
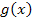ist, hat sie die gleiche Steigung. Die Gerade hat die Steigung 
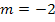und somit auch die Tangente im Punkt 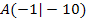. Das bedeutet, dass die gesuchte Funktion bei 
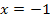die Steigung/erste Ableitung -2 besitzt. Das drückt 
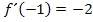aus.
Hier noch einmal die Ansätze für und die erste Ableitung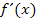 
:
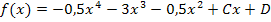
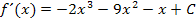
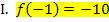
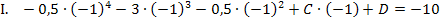
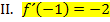
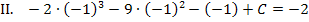
Wir vereinfachen die beiden Gleichungen, indem wir jeweils die linke Seite der Gleichung soweit möglich ausrechnen.
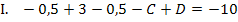
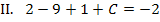
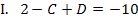
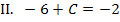
Aus Gleichung II. lässt sich C direkt ermitteln:
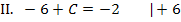
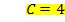
Wir müssen nur noch den soeben berechneten Wert für C in I. einsetzen. Dann lässt sich die zweite Konstante D ausrechnen.
C in I.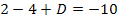 
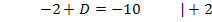
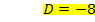
Wir setzen C und D in 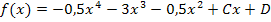ein und erhalten die gesuchte Funktion: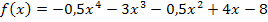
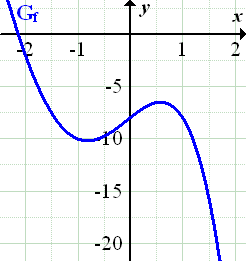
Abb.:Graph 
der Funktion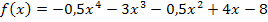
Und nun zum Abschluss noch eine Aufgabe, die schon vielen meiner bisherigen Schülern Probleme bereitet hat. An sich ist sie gar nicht so schwer, nur auf eine Information kommen viele Schüler nicht von selbst. Mal sehen, vielleicht kommst du ja alleine drauf! Falls doch nicht:Die Lösung folgt ja gleich!
