Funktionsgleichungen mit gegebenen Eigenschaften aufstellen und Funktionen modellieren

Dass wirklich 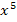als höchste Potenz herauskommen würde, erkennt man auch schon mit folgender Überlegung:

Die Klammer 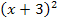ließe sich mit Hilfe der ersten Binomischen Formel 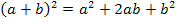ausrechnen;dabei ergäbe sich als höchste Potenz .

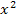Die Klammer 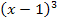könnte entweder mit der Formel 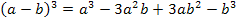(siehe auch:Pascalsches Dreieck) ausgerechnet werden oder auch nach der Umformung 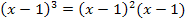mit der zweiten Binomischen Formel 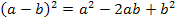und noch einmal mit 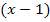multiplizieren. Egal wie man 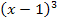ausrechnen würde, es ergäbe sich als höchste Potenz .

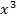Die höchste Potenz des gesamten Polynoms bekommt man, indem man die höchsten Potenzen der einzelnen Faktoren miteinander multipliziert, hier also: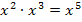

Es kommt also wirklich 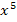als höchste Potenz heraus. Die Funktion 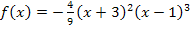ist somit wirklich ein Polynom fünften Grades.

Du möchtest doch noch sehen, wie man die faktorisierte Form 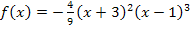durch Ausmultiplizieren auf die Form 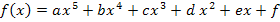bringt? Dann gehe Zu 4. Bsp.:f(x) ausmultiplizieren

Abschließend noch der Graph der Funktion 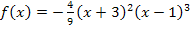, damit du dir die Funktion besser vorstellen kannst. Du kannst an der Stelle 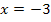die doppelte Nullstelle als Extremum (Tiefpunkt) und bei 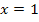die dreifache Nullstelle als Terrassenpunkt des Graphen erkennen.  Im Punkt 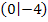schneidet der Graph die y-Achse.

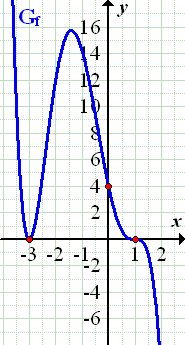
Abb.:Graph der Funktion

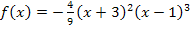
An diesem Beispiel konntest du sehen, dass es sehr einfach ist, die Funktionsgleichung eines Polynoms, also einer ganzrationalen Funktion zu finden, wenn man alle ihre Nullstellen samt Vielfachheit und einen weiteren Kurvenpunkt kennt.

Hättest du dagegen den allgemeinen Ansatz 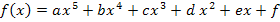für eine Polynomfunktion fünften Grades verwendet, hättest du ein Gleichungssystem mit sechs Gleichungen für sechs Unbekannte lösen müssen. Puh! Das wäre echt extrem viel Rechenaufwand. Das wollen wir uns nicht antun. Aber daran kannst du sehen, wie entscheidend die Wahl des allgemeinen Ansatzes ist.

Merke:Immer wenn die Summe der Vielfachheiten der gegebenen Nullstellen genau dem Grad des Polynoms entspricht, die faktorisierte Form von 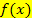verwenden! Dann muss aber noch der Koeffizient a berechnet werden, beispielsweise durch Einsetzen der Koordinaten eines weiteren bekannten Kurvenpunkts.

Nun bleibt noch ein besonderer Fall zu klären. In manchen Aufgaben ist unteranderem die zweite Ableitung 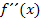einer gesuchten Funktion angegeben. Wie man solche Aufgaben lösen kann, wird an Hand des nächsten Beispiels erklärt.

5. Bsp.:

Von einer Funktion 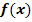ist die zweite Ableitung 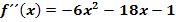bekannt. Der Graph enthält den Punkt 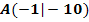. Die Tangente im Punkt 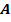an den Funktionsgraph 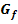verläuft parallel zur Gerade 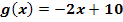. Wie lautet die Funktionsgleichung von ?

---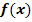