Funktionsgleichungen mit gegebenen Eigenschaften aufstellen und Funktionen modellieren
Bei der einfachen Nullstelle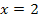 
schneidet der Graph die x-Achse, bei der dreifachen Nullstelle 
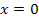ist ein Terrassenpunkt. (Der Terrassenpunkt 
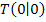war ja im Prinzip schon in der Aufgabenstellung gegeben. Es hießschließlich, dass der Graph im Ursprung einen Terrassenpunkt hat.) Mehr zu den Vielfachheiten der Nullstellen und dem Verlauf des Graphen in der Umgebung der Nullstelle im Kapitel Polynomfunktionen / Ganzrationale Funktionen dritten und höheren Grades.
Im nächsten Beispiel werden wir uns anschauen, wie man die Gleichung einer Polynomfunktion ganz schnell herausfinden kann, wenn alle ihre Nullstellen gegeben sind und die Summe der Vielfachheiten dem Grad des Polynoms entspricht.
4. Bsp.:
Eine Polynomfunktion fünften Grades hat eine doppelte Nullstelle bei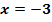 
und eine dreifache Nullstelle bei 
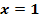. Außerdem liegt der Punkt 
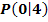auf der Funktion. Ermittle eine Gleichung der Funktion!
Lösung:
Es soll eine Polynomfunktion fünften Grades ermittelt werden, dabei sind eine doppelte und eine dreifache Nullstelle angegeben. Die Vielfachheiten der Nullstellen ergeben zusammen genau den Grad der Polynomfunktion. (Die doppelte Nullstelle hat die Vielfachheit 2, die dreifache Nullstelle hat die Vielfachheit 3. Alle Vielfachheiten miteinander addiert, ergibt 2 + 3 = 5, also den Grad des Polynoms.) Daher kann mit der faktorisierten Form der Funktion gearbeitet werden. Die doppelte Nullstelle ist bei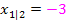 
, die dreifache Nullstelle bei 
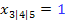. Der Ansatz für 
lautet dann:
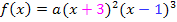
Dir ist nicht klar, wie man auf diesen Ansatz kommt? Dann siehe: Ausführliche Erklärungen zur faktorisierten Form im 4. Bsp.
Jetzt muss nur noch der Koeffizient a berechnet werden. Dazu braucht man noch einen Kurvenpunkt. Laut Angabe liegt der Punkt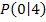 
auf der Funktion. Wir setzen seine Koordinaten einfach in 
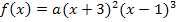ein und lösen dann nach a auf. (Denk´daran, dass nur eine andere Schreibweise für y ist. Der Punkt 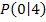liegt auf der Funktion . Daher kann man für die y-Koordinate 4 einsetzen und für x die zugehörige x-Koordinate 0.)
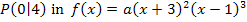eingesetzt, ergibt:
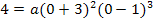
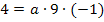
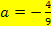
Jetzt muss nur noch der soeben ermittelte Wert für a in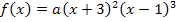 
eingesetzt werden und schon sind wir fertig! Die gesuchte Funktion lautet:
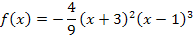
Dies ist die faktorisierte Form der gesuchten Polynomfunktion fünften Grades. Dass es sich bei wirklich um ein Polynom fünften Grades handelt, erkennt man an der faktorisierten Form nur indirekt. Man müsste die Funktion noch ausmultiplizieren, dann würde man als höchste Potenz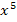 
erhalten. Das Polynom ist also fünften Grades, wie verlangt. Das Ausmultiplizieren der faktorisierten Form ist hier aber sehr viel Arbeit. Daher schenken wir uns das.
