Funktionsgleichungen mit gegebenen Eigenschaften aufstellen und Funktionen modellieren

3. Bsp.:

Der Ursprung ist Terrassenpunkt einer Polynomfunktion vierten Grades. Der Punkt 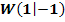ist Wendepunkt der Funktion. Ermittle die Funktionsgleichung!

Lösung:

Gesucht ist eine Polynomfunktion vierten Grades. Daher lautet der allgemeine Ansatz:

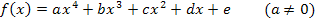
Wir bilden vorweg die ersten beiden Ableitungen. Die zweite Ableitung brauchen wir, da in der Aufgabe von einem Wendepunkt die Rede war.

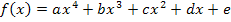
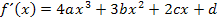
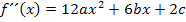
Nun suchen wir die nötigen Informationen aus der Angabe heraus. Wir müssen insgesamt fünf Unbekannte, also die Koeffizienten von a bis e berechnen. Daher benötigen wir fünf Gleichungen, d.h. fünf Informationen. Sie lauten:

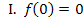
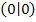Der Ursprung, also der Punkt liegt auf dem Graph.

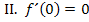
Wegen Terrassenpunkt bei 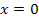waagrechte Tangente, also Steigung 0

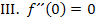
Terrassenpunkt ist auch Wendepunkt, daher bei 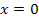Krümmung 0

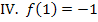
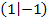Der Punkt liegt auf dem Graph.

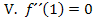
Wegen Wendepunkt bei 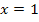Krümmung 0

Nun stellen wir die zugehörigen Gleichungen auf.

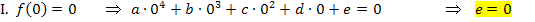
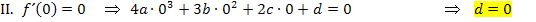
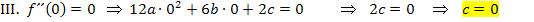
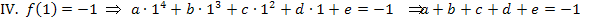
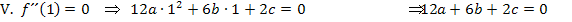
Aus den Gleichungen I., II. und III. ergeben sich direkt die Koeffizienten c, d und e. Wir setzen diese Werte in die Gleichungen IV. und V. ein. Die dadurch entstehenden Gleichungen bezeichnen wir mit IV´. und V´.

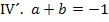
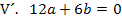
Nun liegen zwei Gleichungen für die zwei Unbekannten a und b vor. Wir verwenden hier das Einsetzungsverfahren, weil sich IV´. so leicht nach einer der beiden Unbekannten auflösen lässt. Ob man nach a oder b auflöst, ist egal. Wir entscheiden uns für das Auflösen nach a.

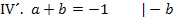
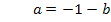
Dies setzen wir jetzt für a in V´. ein. Dadurch fällt a heraus und wir können b berechnen.

a in V´.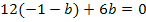

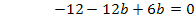
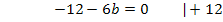
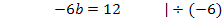
Nun fehlt nur noch die Unbekannte a. Wir erhalten sie, indem wir den berechneten Wert für b in die nach a aufgelöste Form von IV´. einsetzen.

b in IV´.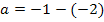

Jetzt haben wir alle Koeffizienten ermittelt: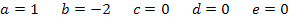

Wir müssen die ermittelten Werte nur noch in den allgemeinen Ansatz 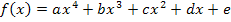einsetzen.

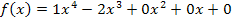
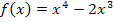
Fertig!

Der Graph der Funktion 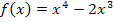ist in der folgenden Abbildung dargestellt.

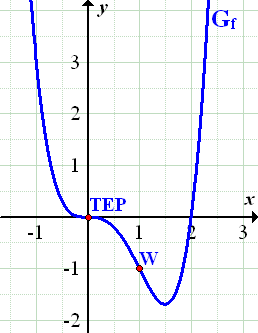
Abb.:Graph der Funktion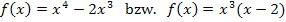

Allgemeine Hinweise zur Funktion :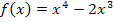

Wenn man die Nullstellen der Funktion 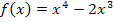berechnen will, muss man nur 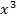ausklammern. Dann liegt die Funktion bereits in ihrer faktorisierten Form vor. Daraus lassen sich die Nullstellen direkt ablesen, weil man einfach die einzelnen Faktoren gleich Null setzen kann.

Ausmultiplizierte Form:         Faktorisierte Form (Produktform):

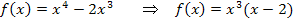
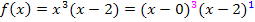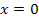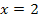Man kann bei der faktorisierten Form von an den Potenzen der einzelnen Faktoren erkennen, dass bei eine Nullstelle und bei eine 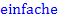Nullstelle vorliegt.

---