Extremwertaufgaben mit Nebenbedingung / Optimierungsprobleme
Erste Seite des neuen Rechtecks in Metern: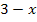 
Zweite Seite des neuen Rechtecks in Metern: y
1. Schritt:Nebenbedingung heraussuchen:
Der Punkt P liegt irgendwo auf der Parabel, wo genau wissen wir noch nicht. P wandert praktisch auf dem Parabelbogen entlang. Die Nebenbedingung ist hier deshalb einfach die Parabelgleichung;sie stellt schließlich einen Zusammenhang zwischen x und y her, wie für eine Nebenbedingung nötig.
Nebenbedingung: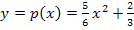 
2. Schritt:Hauptbedingung hinschreiben:
Die Fläche des neuen Rechtecks soll maximal werden. Die Fläche eines Rechtecks berechnet sich bekanntlich nach der Formel „Länge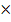 
Breite“. Mit der Länge 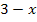und der Breite y ergibt sich für die Fläche des neuen Rechtecks:
Hauptbedingung: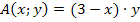 
3. Schritt:Nebenbedingung nach einer Variablen auflösen und in die Hauptbedingung einsetzten:
Die Nebenbedingung ist schon nach y aufgelöst. Sie braucht nur noch in die Hauptbedingung eingesetzt zu werden. So bekommen wir die Zielfunktion. Sie enthält dann nur noch die Variable x.
NB in HB: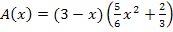 
Zielfunktion
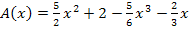
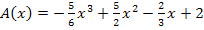
4. Schritt:Definitionsmenge der Zielfunktion:
Dazu stellen wir uns erst einmal die Frage:Wo schneidet die Parabel die obere Kante der ursprünglichen Glasplatte? Die Oberkante der ursprüngliche Platte verläuft in 4 Metern Höhe über der Unterkante der Glasplatte, also entlang der Gerade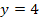 
. Um den Schnittpunkt zu bestimmen, setzt man die Parabel mit 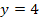gleich.
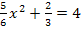
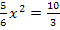
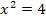
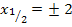
Wegen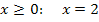 
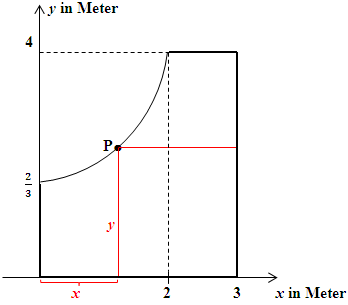
Es macht keinen Sinn, x größer als 2 zu wählen, denn warum sollte man denn mehr als nötig wegschneiden. Wir wollen schließlich eine möglichst große neue Platte erhalten. Die Grenzen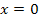 
und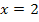 
sind hier noch sinnvoll, denn 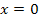entspräche einem waagrechten Schnitt in der Höhe von 
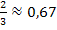Metern über der Unterkante. 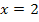entspräche einem senkrechten Schnitt im Abstand 2 Meter von der linken Seitenkante. Beide Grenzen sind daher bei der Definitionsmenge eingeschlossen.
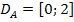
5. Schritt:Extrema der Zielfunktion berechnen:
Hier noch einmal die Zielfunktion: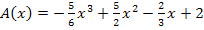
Ableitung bilden: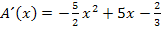 
Ableitung gleich Null setzen: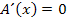 
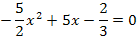
Wir verwenden die Mitternachtsformel.
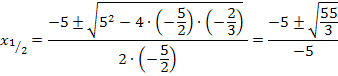
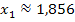
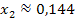
Anmerkung zur Rundung:Es soll laut Angabe auf Millimeter gerundet werden. Da x eine Länge in Metern darstellt, muss auf drei Nachkommastellen gerundet werden.
Beide x-Koordinaten liegen innerhalb von .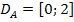
