Extremwertaufgaben mit Nebenbedingung / Optimierungsprobleme
In Abschlussprüfungen der FOS oder BOS darfst du die Definitionsmenge keinesfalls weglassen! (Sonst gibt es ganz sicher Punktabzug. Da ist man auf der FOS / BOS sehr streng.) Sie wird sogar in der Regel explizit in der Aufgabenstellung gefragt. Die Randpunktuntersuchung muss, wie gesagt, nur dann durchgeführt werden, wenn mehrere Extrema innerhalb der Definitionsmenge existieren. Dann gibt es in Prüfungen auf die Randpunktuntersuchung Punkte. Wer sie also vergisst, obwohl sie nötig wäre, bekommt Punktabzug! Gibt es allerdings nur ein einziges Extremum innerhalb der Definitionsmenge, reicht folgende Begründung:„Das Extremum ist das einzige Extremum innerhalb der Definitionsmenge. Die Zielfunktion ist stetig und ändert nur an dieser Stelle ihr Monotonieverhalten. Daher handelt es sich um das absolute Extremum der Zielfunktion.“ Eine gesonderte Randpunktuntersuchung ist dann nicht mehr nötig.
Nun haben wir viel über die Randpunktuntersuchung geredet, aber immer noch kein konkretes Beispiel dafür angeschaut. Also gleich weiter mit dem nächsten Beispiel. Dabei werden die Randpunkte der Definitionsmenge wichtig.
1. Bsp.:Die optimale Glasplatte
Bei einer ursprünglich rechteckigen Glasplatte ist die linke obere Ecke abgebrochen. Die Breite der Glasplatte war ursprünglich 3,0 Meter;ihre Länge war 4 Meter. Die Bruchkante verläuft entlang eines parabelförmigen Bogens. Legt man den Ursprung des Koordinatensystems in die untere linke Ecke der Glasplatte, folgt die Bruchkante der Parabel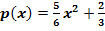 
mit x 
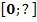. Vergleiche Skizze (nicht maßstabsgetreu)!
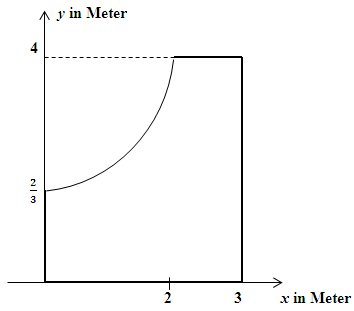
Ein Glaser will aus dieser Glasplatte nun eine neue rechteckige Platte herausschneiden, die einen möglichst großen Flächeninhalt besitzen soll. Wie muss er dazu schneiden? Wie großist der maximale Flächeninhalt? (Runde dabei auf Millimeter genau!)
Lösung:
Bezeichnung der Variablen festlegen:
Der Abstand des senkrechten Schnitts zur linken Seitenkante des ursprünglichen Rechtecks beträgt x Meter und der Abstand des waagrechten Schnitts zur unteren Kante ist y Meter. Vergleiche Skizze!
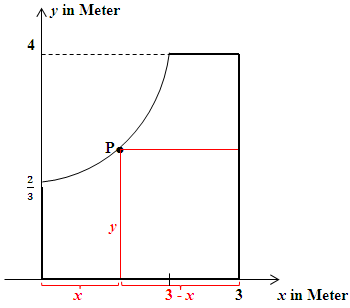
Die roten Linien zeigen eine mögliche Lage der Schnittkanten an. (Die Fläche des neuen Rechtecks ist dabei vermutlich noch nicht maximal. Es wurde einfach ein beliebiges neues Rechteck eingezeichnet, damit du dir die Problematik besser vorstellen kannst.)
x ist die x-Koordinate eines Punktes P auf der Parabel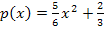 
. Von diesem Punkt ausgehend wurde eine Parallele zur x-Achse und eine zur y-Achse gezeichnet. Diese Linien (in der obigen Skizze rot dargestellt) entsprechen den beiden Schnittkanten.
Wir überlegen uns die Längen der beiden Seiten des neuen Rechtecks. Betrachte dazu noch einmal die obige Skizze!
