Extremwertaufgaben mit Nebenbedingung / Optimierungsprobleme
(Diese Gleichung haben wir erhalten, als wir die Nebenbedingung nach l aufgelöst haben.)
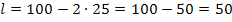
Die Länge der Koppel muss somit 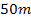 betragen, damit die Fläche der Koppel maximal wird.
betragen, damit die Fläche der Koppel maximal wird.
Hier noch einmal alle Ergebnisse übersichtlich zusammengefasst:
Breite: 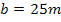
Länge: 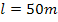
Maximale Fläche: 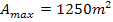
Wenn du dich darüber wunderst, dass die Größe des Flächeninhalts tatsächlich von der Wahl der Länge und Breite des Zaunes abhängt, solltest du mit ein paar anderen Werten für l und b den Flächeninhalt der Koppel ausrechnen und ihn mit dem Wert 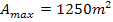 vergleichen. Du wirst feststellen, dass sich wirklich immer Werte ergeben, die kleiner sind als
vergleichen. Du wirst feststellen, dass sich wirklich immer Werte ergeben, die kleiner sind als 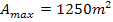 .
.
Würde man beispielsweise für die Breite 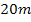 wählen, so blieben für die zugehörige Länge
wählen, so blieben für die zugehörige Länge 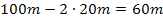 . Der zugehörige Flächeninhalt wäre dann
. Der zugehörige Flächeninhalt wäre dann 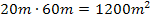 , was offensichtlich keiner ist als
, was offensichtlich keiner ist als 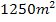 . Du kannst das selbst ruhig noch mit anderen Längen und Breiten nachrechnen;es wird sich immer ein kleinerer Flächeninhalt ergeben als
. Du kannst das selbst ruhig noch mit anderen Längen und Breiten nachrechnen;es wird sich immer ein kleinerer Flächeninhalt ergeben als 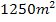 .
.
Leider sind Extremwertaufgaben mit Nebenbedingungen – sie werden auch als Optimierungsprobleme bezeichnet – ziemlich komplex. Wir fassen daher noch einmal alle Schritte zusammen, die nötig sind, um eine Extremwertaufgabe mit Nebenbedingung zu lösen.
| Anleitung zum Lösen von Extremwertaufgaben mit Nebenbedingung:
· Vorweg: Bezeichnung der verwendeten Variablen festlegen · 1. Schritt:Nebenbedingung NB (= Gleichung, die einen Zusammenhang zwischen den Variablen herstellt) aus der Angabe entnehmen. Dazu kann eventuell der Satz des Pythagoras oder der Strahlensatz benötigt werden. Das hängt von der Aufgabe ab. Geht es in der Aufgabe um einen Punkt, der irgendwo auf einer gegebenen Funktion · 2. Schritt:Hauptbedingung HB (= Formel für die Größe, die minimal oder maximal werden soll) aufschreiben. Die schwierigeren benötigten Formeln stehen in der Formelsammlung bzw. auf der Merkhilfe. · 3. Schritt:Nebenbedingung nach einer der Variablen auflösen und in die Hauptbedingung einsetzen. Das ergibt die Zielfunktion. Die Variable, nach der man die Nebenbedingung vorher aufgelöst hat, fällt dabei heraus. Es verbleibt genau die andere als einzige Variable in der Zielfunktion. · 4. Schritt:Sinnvolle Definitionsmenge der Zielfunktion angeben Oft wird nach Streckenlängen, wie z.B. der Seite eines Rechtecks oder Dreiecks, dem Radius oder der Höhe eines Zylinders oder Kegels gefragt. Eine Streckenlänge muss natürlich positiv sein. Ob auch eine Begrenzung der Definitionsmenge nach oben existiert, hängt von der Aufgabe ab, aber die untere Grenze ist meist Null. (Ob die Null aus- oder eingeschlossen ist, muss man sich selbst überlegen.) · 5. Schritt:Extrema der Zielfunktion berechnen Zielfunktion ableiten, Ableitung gleich Null setzen und nach der Variablen auflösen. Dann Art der Extrema überprüfen:Mittels Monotonieuntersuchung oder mit der zweiten Ableitung der Zielfunktion Wenn nur ein einziges Extremum vorhanden ist, ist dies auch das absolute Extremum. Die y-Koordinate des Extrempunktes ergibt dann die gesuchte absolut maximale bzw. minimale Größe. D.h. die berechnete x-Koordinate des Extremums in die Zielfunktion einsetzten und man bekommt die maximale/minimale Fläche, das maximale/minimale Volumen oder die maximale/minimale Streckenlänge etc., je nachdem was gesucht ist. · 6. Schritt:Randpunktuntersuchung (nur notwendig, wenn mehrere Extrema innerhalb der Definitionsmenge existieren) Die Ränder der Definitionsmenge in die Zielfunktion einsetzten, wenn die Ränder noch in der Definitionsmenge eingeschlossen sind bzw. den jeweiligen Grenzwert (limes) ausrechnen, wenn die Ränder ausgeschlossen sind. Die Ergebnisse jeweils mit der y-Koordinate des vorher berechneten Maximums/Minimums vergleichen:Der Punkt mit der größten y-Koordinate ist das absolute Maximum. Der mit der kleinsten y-Koordinate ist entsprechend das absolute Minimum. Daher Vorsicht:Auch ein Randpunkt kann absolutes Extremum und somit die gesuchte Lösung sein! |
Anmerkung:Viele Gymnasial-Lehrer lassen sowohl die Definitionsmenge der Zielfunktion als auch die Randpunktuntersuchung komplett unter den Tisch fallen. Das ist streng genommen natürlich nicht korrekt, denn man kann auf diese Weise ein eventuell vorhandenes Randextremum nicht herausfinden. Du kannst dann allerdings bei Aufgaben, die dein Lehrer selbst ausgesucht oder selbst gestellt hat, davon ausgehen, dass es wohl einfach kein Randextremum gibt. Daher kannst du genauso wie dein Lehrer auf die Schritte 4 (Definitionsmenge) und 6 (Randpunktuntersuchung) vollständig verzichten. Wirklich astrein ist das zwar nicht, doch der Lehrer in der Schule gibt nun mal den Ton an.

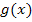 liegen soll, ist die Funktionsgleichung von
liegen soll, ist die Funktionsgleichung von 