Extremwertaufgaben mit Nebenbedingung / Optimierungsprobleme
h. man setzt die beiden Ränder der Definitionsmenge in die Zielfunktion ein und vergleicht die y-Koordinaten der Randpunkte jeweils mit der y-Koordinate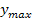 
des berechneten Hochpunktes. Der Punkt mit der größten y-Koordinate ist dann der absolute Hochpunkt. (Bei der Ermittlung des absoluten Minimums geht man entsprechend vor, nur dass der Punkt mit der kleinsten y-Koordinate der absolute Tiefpunkt ist.)
Für die Randpunktuntersuchung benötigt man natürlich die Definitionsmenge. Daher kann man die Definitionsmenge nur dann weglassen, wenn man keine Randpunktuntersuchung machen muss, weil die Zielfunktion sowieso nur ein einziges Extremum hat, was dann zwangsläufig das absolute Extremum darstellt.
5. Schritt:Extrema der Zielfunktion berechnen
Wir haben nun die Zielfunktion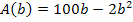 
und ihre Definitionsmenge 
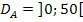ermittelt. Gesucht ist ja diejenige Breite b, bei der sich der größte Flächeninhalt 
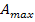ergibt. Wir suchen also das absolute Maximum der Zielfunktion. Der absolute Hochpunkt der Funktion 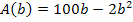hat schließlich den absolut größten Funktionswert, was hier dem absolut größten Flächeninhalt 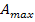entspricht.
Wie man die Extrema einer Funktion berechnet, weißt du sicherlich:Man leitet die Zielfunktion ab und setzt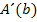 
gleich Null. So findet man alle vorhandenen Extrempunkte, also die relativen und absoluten Extrema. Die Art der Extrema, also ob ein HOP oder TIP vorliegt, kann dann entweder mit Hilfe des Monotonieverhaltens oder mit der zweiten Ableitung untersucht werden. (Zweite Ableitungnur verwenden, wenn ihr das in der Schule schon besprochen habt.) In diesem Beispiel gibt es sowieso nur ein einziges Extremum, wie du gleich sehen wirst. Daher muss es sich auch um das absolute Extremum handeln. (Wie man mittels Randpunktuntersuchung einen absoluten Hochpunkt bzw. Tiefpunkt findet, wenn mehrere Extrema innerhalb der Definitionsmenge existieren, wird an Hand eines anderen Beispiels weiter unten gezeigt.)
Berechne doch gleich mal selbst das Extremum unserer Zielfunktion 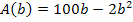! Das ist wirklich nicht schwer. Du kannst dein Ergebnis dann mit der folgenden Lösung vergleichen.
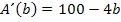
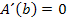
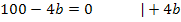
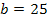
Nun wissen wir, dass nur bei 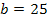ein Extremum der Zielfunktion vorliegt. Es handelt sich somit um das einzige Extremum, also um das absolute Extremum. (Deswegen entfällt hier die Randpunktuntersuchung.) Es muss nur noch gezeigt werden, dass es sich tatsächlich um ein Maximum handelt. Wir überprüfen nun die Art des Extremums.
1. Methode:Mit der zweiten Ableitung (Nur für Schüler, die das im Unterricht schon gelernt haben. Alle anderen verwenden bitte die 2. Methode. Siehe unten!
