Extremwertaufgaben mit Nebenbedingung / Optimierungsprobleme
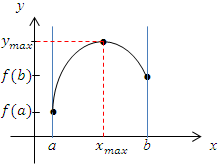
Abb.:Graph einer Funktion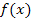 
, die nur ein einziges Extremum (hier:Maximum) innerhalb der Definitionsmenge 
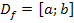hat. Das Maximum 
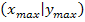ist das absolute Maximum. Beide Randpunkte 
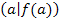und 
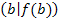liegen tiefer.
Damit einer der Randpunkte höher liegen könnte, müsste der Graph seine Monotonie, d.h. sein Steigungsverhalten, noch einmal irgendwo ändern. Er müsste z.B. irgendwo rechts vom Hochpunkt noch einmal steigen. Dann gäbe es aber zusätzlich zum Hochpunkt einen Tiefpunkt, also ein weiteres Extremum innerhalb der Definitionsmenge. Wir haben jedoch gesagt, dass es sich um eine Funktion mit nur einem einzigen Extremum handeln soll. Dabei ändert sich die Monotonie nur bei dem Extremum. Daher ist ein einziges Extremum immer ein absolutes Extremum.
Wenn die Zielfunktion innerhalb ihrer Definitionsmenge nur ein einziges Extremum besitzt, ist dies sicher das absolute Extremum. Eine zusätzliche Randpunktuntersuchung ist nicht nötig. Die Randpunkte der Definitionsmenge müssen also gar nicht extra berechnet und mit dem Extremum verglichen werden.
Anders sieht das bei einer Funktion aus, die mehrere Extrema innerhalb der Definitionsmenge besitzt. Hat eine Funktion innerhalb ihrer Definitionsmenge beispielsweise einen Hochpunkt und einen Tiefpunkt, so kann einer der Randpunkte höher liegen als der Hochpunkt. Betrachte dazu die beiden folgenden Abbildungen!
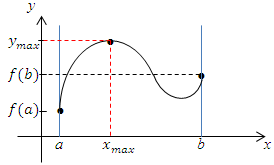
Abb.:Graph einer Funktion 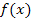, die mehrere Extrema (hier:je ein Maximum und ein Minimum) innerhalb der Definitionsmenge 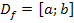hat. Der Hochpunkt 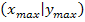ist hier tatsächlich der absolute Hochpunkt, weil beide Randpunkte 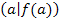und 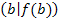tiefer liegen. Das absolute Maximum, also der absolut größte Funktionswert, der angenommen werden kann, liegt wirklich bei 
.
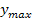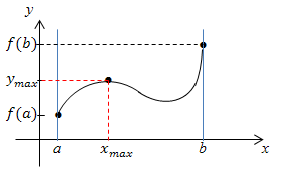
Abb.:Graph einer Funktion 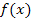, die mehrere Extrema (hier:je ein Maximum und ein Minimum) innerhalb der Definitionsmenge 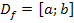hat. Der Punkt 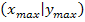ist hier nicht der absolute Hochpunkt, sondern nur ein relativer Hochpunkt. Der Randpunkt 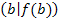liegt höher als der Punkt 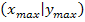. Hier ist der Randpunkt 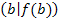der absolute Hochpunkt. Das absolute Maximum, also der absolut größte Funktionswert, der angenommen werden kann, liegt bei 
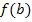und nicht bei .
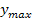Man kann daher bei einer Funktion, die mehrere Extrema innerhalb der Definitionsmenge besitzt, nicht generell sagen, ob der berechnete Hochpunkt selbst der absolute Hochpunkt ist oder etwa einer der Randpunkte. Man muss dann unbedingt eine Randpunktuntersuchung durchführen, d.
