Extremwertaufgaben mit Nebenbedingung / Optimierungsprobleme
Es fällt schließlich immer diejenige Variable heraus, nach der man die Nebenbedingung aufgelöst hat. Ist die Zielfunktion nicht als Zwischenergebnis angegeben, kannst du frei wählen, nach welcher Variablen du die Nebenbedingung auflösen willst.
4. Schritt:Definitionsmenge der Zielfunktion angeben
Die Zielfunktion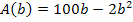 
ist nicht für alle reellen Zahlen definiert. Für b können einerseits nur positive Werte eingesetzt werden, da b schließlich für die Breite in Metern steht. Andererseits kann b aber auch nur Werte unter 50 annehmen, da insgesamt nur 100 m Zaun zur Verfügung stehen. Wäre b nämlich gleich 50, dann bliebe kein Zaun mehr für die Länge. Für 
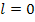ergibt sich jedoch kein Rechteck mehr. Wäre b länger als 50, bräuchte man mehr als 100 m Zaun;das geht hier also auch nicht. Daher gilt:b kann nur Werte über 0 und unter 50 annehmen.
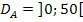
Die Definitionsmenge kann natürlich auch durch Rechnung ermittelt werden. Sowohl b als auch l müssen positiv sein, da es sich um die Seitenlängen des Rechtecks handelt. (Eine Streckenlänge ist schließlich immer positiv.)
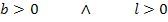
Aus der Nebenbedingung wissen wir, dass gilt: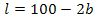 
Das setzten wir jetzt für l ein, damit nur noch b in den Ungleichungen vorkommt. Wir wollen ja herausfinden, was für b in die Zielfunktion 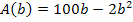eingesetzt werden darf.
Jetzt lösen wir die hintere Ungleichung nach b auf.
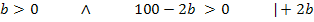
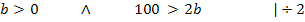
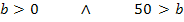
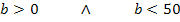
Nun haben wir rechnerisch ermittelt, dass b größer als 0 aber auch kleiner als 50 sein muss. So kommt man auch zu der Definitionsmenge 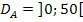, die wir vorher schon durch bloße Überlegung gefunden haben.
Die Definitionsmenge der Zielfunktion ist nicht bei allen Extremwertaufgaben mit Nebenbedingungen relevant. Daher lassen manche Lehrer die Definitionsmenge auch einfach weg. Das ist allerdings gefährlich, da bei diesen Aufgaben nach dem absoluten Extremum gefragt ist und das kann auch mal einer der Randpunkte sein. Als Randpunkte bezeichnet man die Punkte am Rand der Definitionsmenge. (Ob die Punkte gerade noch zur Funktion gehören oder nicht, hängt davon ab, ob die Grenzen der Definitionsmenge eingeschlossen oder ausgeschlossen sind.)
Hat eine Funktion innerhalb ihrer Definitionsmenge nur ein einziges Extremum, ist dieses Extremum automatisch das absolute (globale) Extremum der Funktion. Betrachten wir beispielsweise eine Funktion, die nur ein einziges Maximum und sonst keine weiteren Extrema (innerhalb der Definitionsmenge) besitzt. Bei so einer Funktion ist dieses Maximum sicher das absolute Maximum. Ein absoluter Hochpunkt ist schließlich der Kurvenpunkt, der am allerhöchsten liegt. Die Randpunkte liegen zwangsläufig tiefer, da sich die Monotonie nur beim Extremum ändert. Vergleiche dazu die folgende Abbildung!
