Extremwertaufgaben mit Nebenbedingung / Optimierungsprobleme

Hier noch einmal die erste Ableitung: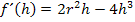

Zweite Ableitung: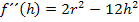

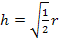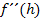Wir setzen in ein und bestimmen das Vorzeichen des Ergebnisses. Wir arbeiten mit 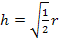und nicht mit 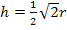, da dies praktischer ist. 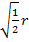lässt sich nämlich leichter quadrieren als .

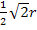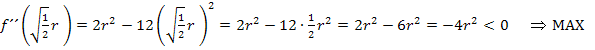
Es handelt sich um ein Maximum, da die zweite Ableitung an dieser Stelle negativ ist. Da es sich um das einzige Extremum innerhalb der Definitionsmenge handelt, muss es sich um das absolute Maximum handeln.

Wir wissen nun, dass bei 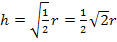das absolute Maximum der Ersatzzielfunktion 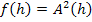liegt. Somit muss auch die Zielfunktion 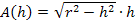an der Stelle 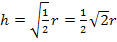ihr absolutes Maximum haben. Die Randpunktuntersuchung (6. Schritt) ist somit unnötig und entfällt.

Wir berechnen nun die maximale Fläche 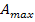, indem wir den berechneten Wert für h in die Zielfunktion 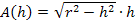einsetzen.

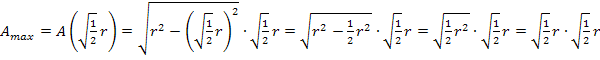
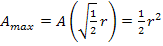
Nun fehlt nur noch die zugehörige Grundlinie. Man erhält sie durch Einsetzen des berechneten Wertes von h in die Nebenbedingung .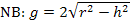

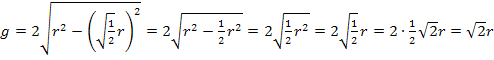
Damit ist die Aufgabe gelöst. Interessant ist dabei das Verhältnis zwischen Höhe und Grundlinie des Dreiecks MAB mit maximaler Fläche. Die Höhe 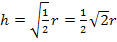ist genau die Hälfte der Grundlinie 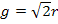. Daher beträgt das Verhältnis h :g unabhängig vom Radius r des Halbkreises immer 1 :2.

Es gibt noch viele andere interessante Aufgabenbeispiele zum Thema Extremwertaufgaben, doch wollen wir es hier mit den bereits vorgestellten Aufgaben bewenden lassen. Das Prinzip hast du hoffentlich inzwischen verstanden. Jetzt hilft nur noch eines:Üben, üben und noch einmal üben! Das kann dir niemand abnehmen.

---