Extremwertaufgaben mit Nebenbedingung / Optimierungsprobleme
Lösung:
Bezeichnung der Variablen festlegen:
Die Bezeichnung der Variablen ist in der Aufgabenstellung bereits festgelegt.
Grundlinie des Dreiecks:g
Höhe des Dreiecks:h
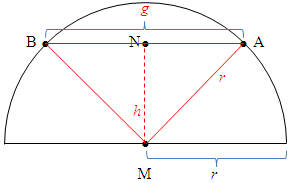
Damit wir uns das alles besser vorstellen können, fertigen wir erst mal eine Skizze an. Der Radius r des Halbkreises ist leider nicht gegeben, er ist aber auch nicht gesucht. Wir müssen deshalb nachher in Abhängigkeit von r rechnen, d.h. wir tun so, als wenn r eine konkrete Zahl wäre. In den Ergebnissen darf r ruhig noch vorkommen. Für die Zeichnung müssen wir uns selbst etwas für r ausdenken.
Vorsicht:r ist hier keine Variable, sondern ein Parameter, also eine Konstante!
Was bedeutet das? Ganz einfach:Wir kennen r zwar nicht, aber das macht nichts. Wir tun einfach so, als wäre r eine feste Zahl. Denk dir beispielsweise r = 4cm oder r = 5cm. Du darfst jedoch in den nachfolgenden Rechnungen nicht wirklich etwas für r einsetzen, du sollst aber rechnen, als wäre r zum Beispiel 4cm. Für unsere Skizze nehmen wir hier:r = 4cm
Wenn du die Aufgabe alleine löst, kannst du dir natürlich auch einen anderen Wert für r aussuchen. Die Länge 4cm bietet sich einfach an, da die Zeichnung damit nicht zu klein, aber auch nicht zu großwird. Den Mittelpunkt von [BA] nennen wir im Folgenden N.
1. Schritt:Nebenbedingung aufschreiben
Die Nebenbedingung ist ja eine Gleichung, die einen Zusammenhang zwischen den Variablen, hier g und h, herstellt. Aus der Zeichnung geht hervor, dass im Teildreieck MAN der Satz des Pythagoras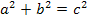 
gilt, da das Dreieck MAN rechtwinklig ist. Die Hypotenuse (= Seite gegenüber des rechten Winkels) ist hier die Seite [MA]. Die Länge von [MA] entspricht also dem c aus dem Satz des Pythagoras. (c steht ja im Satz des Pythagoras für die Länge der Hypotenuse, a und b dagegen für die Längen der Katheten eines rechtwinkligen Dreiecks.) Die Katheten sind hier [MN] und [NA].
Nun wenden wir im Dreieck MAN den Satz des Pythagoras an. (Man hätte natürlich auch das Dreieck MNB nehmen können.)
Pythagoras im △MAN: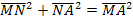 
An der Zeichnung kann man erkennen, dass für die einzelnen Streckenlängen gilt:
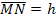
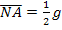
Damit ergibt sich die Nebenbedingung:
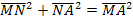
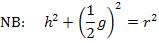
2. Schritt:Hauptbedingung aufstellen
Die Fläche des Dreiecks MAB soll maximal werden. Wir brauchen also die Formel für den Flächeninhalt eines Dreiecks.
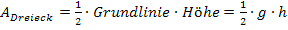
Im Dreieck MAB hat die Grundlinie [BA] die Länge g und die Höhe [MN] die Länge h.
Daher lautet die Hauptbedingung:
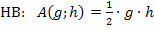
3. Schritt:Nebenbedingung nach einer Variablen auflösen und in die Hauptbedingung einsetzten:
