Extremwertaufgaben mit Nebenbedingung / Optimierungsprobleme
Es gilt somit:
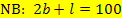
Diese Gleichung stellt hier die Nebenbedingung (NB) dar.
2. Schritt:Hauptbedingung aufstellen
Die Hauptbedingung ist eine Formel für diejenige Größe, die maximal (oder minimal) werden soll. (Oft steht diese Formel auch in der Formelsammlung oder der Merkhilfe für G8. Beispielsweise die Formel für das Volumen eines Zylinders, wenn das Volumen eines Zylinders maximal werden soll, oder die Formel für die Oberfläche eines Kegels, wenn die Kegeloberfläche minimal werden soll.) In dieser Formel dürfen nur diejenigen Variablen vorkommen, die man vorher festgelegt hat, aber keine anderen Variablen. Also nicht plötzlich für die Länge beispielsweise a schreiben, sondern bei den oben festgelegten Bezeichnungen l für die Länge und b für die Breite bleiben. In diesem Aufgabenbeispiel soll die Fläche des Rechtecks mit der Länge l und der Breite b maximal werden. Die Formel für die Fläche eines Rechtecks lautet bekanntlich „Länge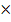 
Breite“. Die Hauptbedingung (HB) ist deshalb:
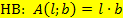
3. Schritt:Nebenbedingung (NB) nach irgendeiner der Variablen auflösen, in die Hauptbedingung (HB) einsetzen und soweit möglich vereinfachen
Hier noch einmal die Nebenbedingung, die wir im 1. Schritt ermittelt haben:
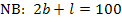
Diese Gleichung lässt sich leichter nach l auflösen als nach b. Daher lösen wir nach l auf.
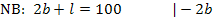
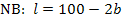
Das setzten wir jetzt in die Hauptbedingung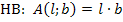 
für l ein. Dadurch fällt die Variable l heraus. Es fällt immer die Variable weg, nach der man vorher aufgelöst hat.
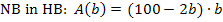
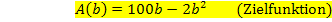
Das ist die benötigte Zielfunktion, also diejenige Funktion, deren absolutes Extremum (hier:Maximum) gesucht ist. Die Funktion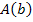 
beschreibt den Zusammenhang zwischen der Breite b unserer Koppel und dem Flächeninhalt der Koppel 
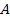. Du bist wahrscheinlich eher an Funktionen der Form 
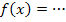gewöhnt. Bei 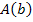entspricht das b einfach dem x von 
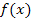. Die Variable ist hier also nicht mehr x, sondern eben b, und die Funktion heißt nicht mehr 
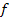, sondern 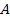. Auf jeden Fall haben wir nun eine Funktion vorliegen, die nur noch eine Variable enthält. Von so einer Funktion können wir das Extremum ermitteln. Wir suchen schließlich die maximale Fläche und die zugehörige Breite. Wir müssen daher im Folgenden mit Hilfe der Ableitung 
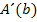das Maximum von 
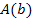berechnen.
Hinweis:In manchen Aufgaben ist die Zielfunktion als Zwischenergebnis angegeben. Dann musst du genau schauen, welche der beiden Variablen noch im Term der Zielfunktion vorkommt. Nach genau der anderen Variablen musst du die Nebenbedingung auflösen, damit du auf die angegebene Zielfunktion kommst.
