Extremwertaufgaben mit Nebenbedingung / Optimierungsprobleme
(Würde man diese Umformung nicht vornehmen, müsste man die Ableitung von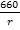 
mit Hilfe der Quotientenregel bilden, weil die Variable r im Nenner steht. Das wäre jedoch wesentlich mehr Arbeit.)
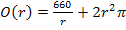
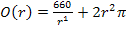
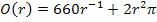
In dieser Form lässt sich die Zielfunktion gut ableiten.
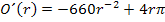
Wir formen die Ableitung mit Hilfe des Potenzgesetzes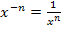 
in einen Bruch um, da man sie so leichter gleich Null setzen kann.
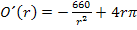
Wir bringen nun alles auf einen gemeinsamen Nenner. Dazu Erweitern wir den hinteren Teil mit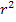 
.
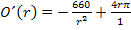
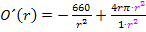
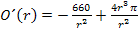
Nun haben beide Brüche den gleichen Nenner. Wir können alles auf einen gemeinsamen Bruchstrich schreiben.
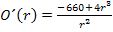
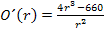
Nun setzen wir die Ableitung gleich Null, um die Extrema zu ermitteln.
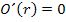
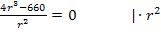
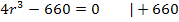
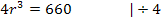
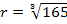
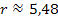
Art des Extremums untersuchen:
Wir müssen jetzt nachweisen, dass die Zielfunktion bei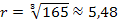 
ein Maximum hat. Das können wir entweder mit Hilfe der Monotonie oder mit der zweiten Ableitung machen. Wir entscheiden uns hier für die Methode mit der zweiten Ableitung. Das geht hier am schnellsten.
Hier noch einmal die erste Ableitung: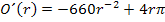
In dieser Form von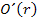 
lässt sich 
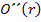am schnellsten bilden, weil man die Ableitungsregel 
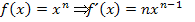verwenden kann.
Zweite Ableitung: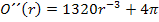 
Wir formen den vorderen Teil von 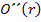noch mit dem Potenzgesetzes 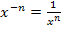in einen Bruch um.
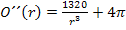
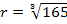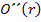Nun setzen wir in ein und ermitteln das Vorzeichen. Damit ein Minimum vorliegt, muss das Vorzeichen positiv sein.
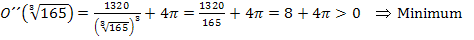
Wir haben nun nachgewiesen, dass sich für 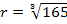ein Minimum der Oberfläche ergibt. Da es sich um das einzige Extremum handelt, ist es auch das absolute Minimum. Die Randpunktuntersuchung (6. Schritt) ist unnötig.
Wir müssen nun noch den minimalen Oberflächeninhalt ermitteln. Dazu brauchen wir nur den berechneten Wert 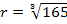in die Zielfunktion 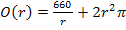einsetzen.
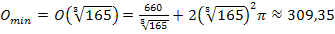
Der minimale Oberflächeninhalt beträgt somit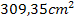 
.
Das einzige, was jetzt noch fehlt, ist die Höhe h, die zum Radius 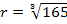gehört. Sie wird berechnet, indem man 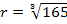in die nach h aufgelöste Nebenbedingung 
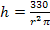einsetzt.
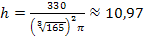
Bei einer Höhe von ungefähr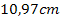 
und einem Radius von 
, also ungefähr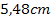 
ergibt sich der minimale Oberflächeninhalt von circa 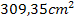. Fertig!
5. Bsp.:
In einen Halbkreis mit Radius r (mit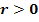 
) wird ein gleichschenkliges Dreieck MAB gezeichnet, dessen Spitze mit dem Mittelpunkt M des Halbkreises zusammenfällt. Die Ecken A und B liegen auf dem Halbkreis. Wie müssen Grundlinie g und Höhe h des Dreiecks gewählt werden, damit die Fläche des Dreiecks maximal wird? Ermittle auch die maximale Fläche des Dreiecks!
