Extremwertaufgaben mit Nebenbedingung / Optimierungsprobleme

Merkhilfe für G8 findest du die Formel für das Volumen eines Zylinders. Sie lautet:

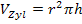
Wenn man das angegebene Volumen (in 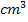) in die Formel einsetzt, erhält man die Nebenbedingung.

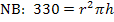
2. Schritt:Hauptbedingung aufstellen

Die Oberfläche der zylindrischen Dose soll möglichst klein werden. Wir brauchen also eine Formel für den Oberflächeninhalt eines geraden Kreiszylinders. (Ein gerader Kreiszylinder ist ein „normaler“ Zylinder, also ein Zylinder mit kreisförmiger Grundfläche, bei dem die Mantellinien senkrecht zur Grundfläche verlaufen.) In der Merkhilfe für G8 bzw. FOS oder BOS in Bayern steht nur die Formel für die Mantelfläche eines geraden Kreiszylinders, jedoch nicht die Formel für seine Oberfläche. Die Oberfläche setzt sich aus der Mantelfläche und den zwei kreisförmigen Grundflächen zusammen. Du musst dir die Oberflächenformel daher selbst zusammenbasteln aus der Formel für die Mantelfläche eines Zylinders 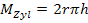und zweimal der Grundfläche, d.h. aus der Formel für den Flächeninhalt eines Kreises .

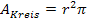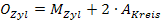
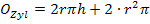
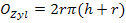
Die Formel enthält die beiden Variablen r und h. Daher schreiben wir als Hauptbedingung:

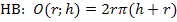
3. Schritt:Nebenbedingung nach einer Variablen auflösen und in die Hauptbedingung einsetzten:

Wir lösen die Nebenbedingung 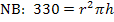nach der Variablen h auf. Das ist geschickter als nach r aufzulösen, denn man müsste die Wurzel ziehen, um nach r aufzulösen. Löst man nach h auf, braucht man keine Wurzel.

NB nach h auflösen:

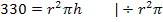
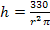
Nun setzen wir diesen Ausdruck für h in die Hauptbedingung 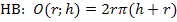ein. So erhalten wir die Zielfunktion. Sie enthält nur noch die Variable r. Die Variable h fällt dabei heraus.

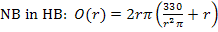
Dies ist bereits die Zielfunktion. Wir vereinfachen sie aber noch etwas. D.h. wir multiplizieren die Klammer aus.

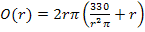
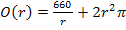
4. Schritt:Definitionsmenge der Zielfunktion angeben

Da es sich bei r um den Radius, also um eine Streckenlänge handelt, muss r positiv sein. Deshalb gilt auf jeden Fall: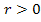

Die Höhe h muss ebenfalls positiv sein. Der Ausdruck 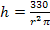ist aber wegen der geraden Potenz von r sowieso für jeglichen Werte von r positiv. Es gibt also keine weitere Einschränkung für r.

Somit ist die Definitionsmenge der Zielfunktion: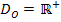

5. Schritt:Extrema der Zielfunktion 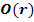berechnen

Hier noch einmal die Zielfunktion: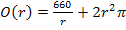

Mit Hilfe des Potenzgesetzes 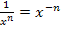formen wir den vorderen Teil der Zielfunktion noch so um, dass wir nachher die Ableitungsregel 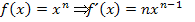anwenden können.

---