Extremwertaufgaben mit Nebenbedingung / Optimierungsprobleme
Dazu verwenden wir die Quotientenregel. (Siehe auch:Weitere Ableitungsregeln)
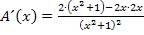
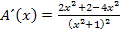
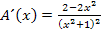
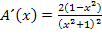
Nun setzten wir die Ableitung gleich Null.
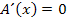
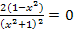
Ein Bruch ist gleich Null, wenn der Zähler gleich Null ist, aber der Nenner nicht gleich Null ist. Der Nenner ist hier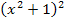 
;er kann gar nicht gleich Null werden. Wir können also einfach den Zähler der Ableitung gleich Null setzen. Das entspricht auch dem Multiplizieren der Gleichung mit dem Nenner. Auf der rechten Seite der Gleichung bleibt die Zahl 0, da Null mit dem Nenner 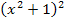multipliziert wieder Null ergibt.
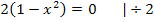
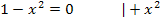
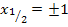
Wegen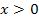 
fällt der negative Wert weg. Es ergibt sich als einzige Lösung:
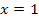
Das ist die x-Koordinate des gesuchten Eckpunktes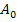 
. Streng genommen müssen wir erst noch nachweisen, dass die Zielfunktion 
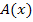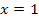für ein Maximum hat, also dass die Fläche des Dreiecks für 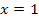maximal wird. Daher machen wir jetzt eine Monotonieuntersuchung von 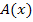. Dabei gilt natürlich: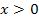
Hier noch einmal die Ableitung: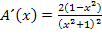
Wir fertigen eine Tabelle der folgenden Form an:
| x |  |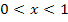
 |
 |
 |
 |
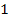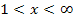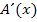0 | |
 |
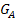Der Nenner der Ableitung ist sowieso immer positiv;das Vorzeichen von 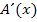hängt somit nur vom Zähler ab. Nur an der Stelle 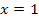ist die Ableitung gleich Null. Deshalb kann sich an dieser Stelle das Vorzeichen der Ableitung ändern. Um jeweils die Vorzeichen von 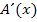in den beiden Teilbereichen 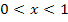und 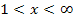zu ermitteln, wählen wir einfach eine konkrete Zahl einmal aus dem einen Bereich und einmal aus dem anderen, setzten sie in den Zähler von 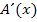ein und bestimmen das jeweilige Vorzeichen. (Den Nenner der Ableitung kann man vernachlässigen;er ist ja immer positiv, egal was für x eingesetzt wird.)
Für 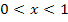kann z.B. 
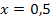verwendet werden. Dann ergibt sich für den Zähler der Ableitung 
:
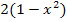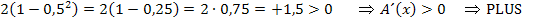
Für 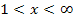kann z.B. 
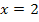verwendet werden. Dann ergibt sich für den Zähler der Ableitung :
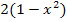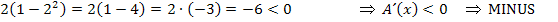
Jetzt tragen wir die entsprechenden Vorzeichen in die Monotonietabelle ein und überlegen uns, was das für das Steigungsverhalten, also für die Monotonie, der Zielfunktion bedeutet.
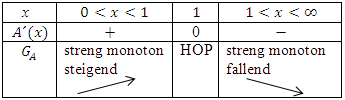
Da der Graph 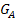links von der 1 steigt 
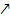und rechts von der 1 fällt 
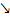, muss an der Stelle x = 1 ein Hochpunkt vorliegen. Es handelt sich um den absoluten Hochpunkt, da es sich um das einzige Extremum der Funktion 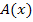handelt. Nur an der Stelle x = 1 ändert sich das Vorzeichen von 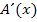. Deshalb kann kein anderer Punkt der Funktion 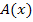höher liegen als der ermittelte Hochpunkt.
