Extremwertaufgaben mit Nebenbedingung / Optimierungsprobleme
Wenn dir das nicht so ganz klar ist, gib doch einfach zwei verschiedene Wurzeln in den Taschenrechner ein, z.B.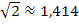 
und 
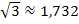. Du siehst, dass das Ergebnis der Wurzel kleiner ist, wenn die Zahl unter der Wurzel kleiner ist. In unserem Beispiel ist also 
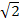kleiner als 
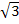, weil 2 kleiner als 3 ist. Dies ist nicht nur in diesem Beispiel so, sondern immer. Je kleiner die Zahl unter der Wurzel (der Radikand) ist, desto kleiner ist auch die Wurzel daraus. Das ist der Grund, warum wir die Wurzel erst mal weglassen können und einfach denjenigen Wert von x ermitteln, für den die wesentlich einfacher abzuleitende quadratische Funktion 
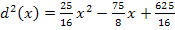ihr Minimum annimmt. Wir geben dieser Funktion noch eine andere Bezeichnung;statt 
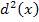schreiben wir hier 
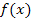. Damit gilt:
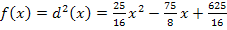
Dies ist nun unsere Ersatz-Zielfunktion. Man kann 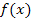wirklich viel einfacher ableiten als die eigentliche Zielfunktion 
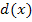, weil man die Kettenregel nicht braucht, um 
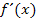zu bilden.
4. Schritt:Definitionsmenge der Zielfunktion und der Ersatzzielfunktion:
Die Punkte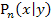 
können überall auf der Gerade 
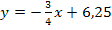liegen. Somit kann die x-Koordinate von P, also x beliebige reelle Zahlen annehmen. Die Definitionsmenge von 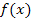bzw. 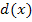ist deshalb:
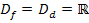
5. Schritt:Extrema der Ersatz-Zielfunktion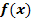 
berechnen
| 
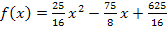
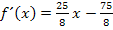
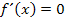
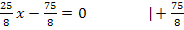
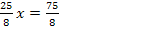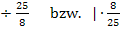
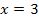
Art des Extremums überprüfen:
Die Funktion 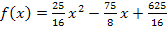ist eine Funktion der Form 
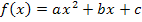, also eine quadratische Funktion, d.h. eine Parabel. Du weißt bestimmt, dass man den Extrempunkt einer Parabel Scheitel nennt. Da es sich bei 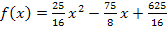offensichtlich um eine nach oben geöffnete Parabel handelt, muss der Scheitel der Parabel ihr absoluter Tiefpunkt sein. (Die Parabel ist nach oben geöffnet, weil die Zahl vor dem 
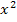positiv ist. Näheres dazu bei Quadratische Funktionen) Weitere Rechnungen wie Monotonieuntersuchung oder zweite Ableitung entfallen deshalb. Bei 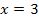nimmt die Funktion 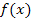ihr absolutes Minimum an.
Jetzt kennen wir die x-Koordinate des Geradenpunktes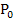 
, der vom Ursprung die kleinste Entfernung besitzt. Seine y-Koordinate erhalten wir, wenn wir die x-Koordinate von 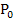, also 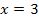, in die Geradengleichung 
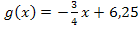einsetzten.
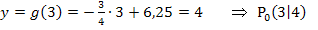
Berechnung des minimalen Abstands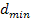 
:
Um den minimalen Abstand des Geradenpunktes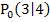 
vom Ursprung zu ermitteln, muss 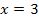in die echte Zielfunktion 
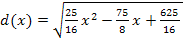eingesetzt werden und nicht in die Ersatz-Zielfunktion 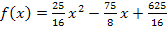. Nur 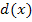beschreibt wirklich den Abstand der Punkte 
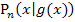vom Ursprung. 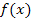ist ja das Quadrat dieses Abstands und nicht der Abstand selbst. Wir müssen daher 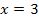in die echte Zielfunktion 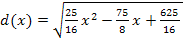einsetzen, um den minimalen Abstand 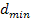zu erhalten.
