Extremwertaufgaben mit Nebenbedingung / Optimierungsprobleme
Man kann diesen Abstand entweder mit Hilfe des Satzes von Pythagoras oder mit Hilfe des Betrags (d.h. der Länge) des Vektors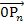 
berechnen. (Siehe auch:Betrag eines Vektors (= Länge eines Vektors) 
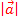) Da einige Schüler bis zum jetzigen Zeitpunkt Vektoren noch nicht gelernt haben, werden wir im Folgenden den Weg mit dem Pythagoras verwenden.
Zur Erinnerung:Satz des Pythagoras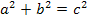 
, wobei a und b die Katheten eines rechtwinkligen Dreiecks darstellen und c die Hypotenuse (= Seite gegenüber des rechten Winkels).
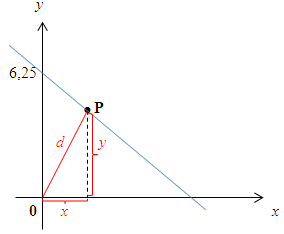
Man erkennt an dieser Skizze, dass der Abstand d der Hypotenuse entspricht;die Katheten sind x und y. Somit gilt:
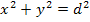
Wir lösen nach d auf, indem wir die Wurzel ziehen.
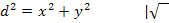
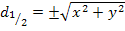
Weil d eine Länge darstellt, muss d positiv sein: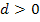 
Deshalb können wir uns das Plus/Minus vor der Wurzel sparen.
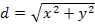
In diesem Ausdruck kommen die beiden Variablen x und y vor. Der Abstand d ist also in Abhängigkeit von x und y dargestellt. Deshalb schreiben wir:
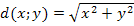
Das ist hier die Hauptbedingung.
3. Schritt:Nebenbedingung nach einer Variablen auflösen und in die Hauptbedingung einsetzten:
Die Nebenbedingung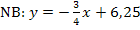 
ist schon nach y aufgelöst. Sie braucht nur noch in die Hauptbedingung 
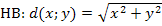eingesetzt zu werden. So bekommen wir die Zielfunktion. Sie enthält dann nur noch die Variable x.
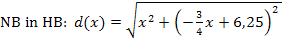
Dies ist schon die Zielfunktion. Wir vereinfachen sie aber erst noch. Wir lösen die Klammer unter der Wurzel auf. Vorsicht:Es handelt sich hier um eine binomische Formel! Damit es sich leichter rechnet, drehen wir vorweg die Reihenfolge in der Klammer um. Dabei muss man natürlich die Vorzeichen „mitnehmen“. Dann ergibt sich die zweite binomische Formel.
Zur Wiederholung:
2. Binomische Formel: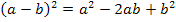 
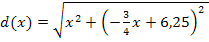
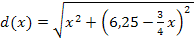
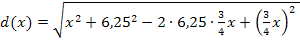
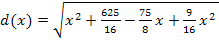
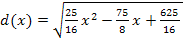
Dies ist eigentlich die Zielfunktion in ihrer komplett vereinfachten Form. Leider ist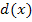 
eine Wurzelfunktion, die sich nicht so einfach ableiten lässt. Man bräuchte zum Ableiten von 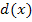die Kettenregel. (Näheres dazu bei:Die Kettenregel) Mit Hilfe eines kleinen Tricks können wir die Aufgabe jedoch wesentlich einfacher lösen. Wir verwenden statt der Wurzelfunktion 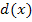ihr Quadrat 
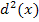. Wir lassen also praktisch die Wurzel weg und arbeiten bloßmit der quadratischen Funktion 
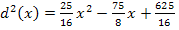. Warum man das machen darf? Wir suchen eigentlich denjenigen Wert von x, wo der Abstand 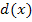minimal wird. Wird der Ausdruck unter der Wurzel minimal, wird auch das Ergebnis der Wurzel minimal.
