Extremwertaufgaben mit Nebenbedingung / Optimierungsprobleme

Die Randpunktuntersuchung muss hier zwangsläufig durchgeführt werden, da ja auch einer der Randpunkte der absolute Hochpunkt sein könnte;es gibt in diesem Beispiel schließlich mehrere (zwei) Extrema innerhalb des Definitionsbereichs. (Gäbe es nur ein einziges Extremum innerhalb der Definitionsmenge, hätte man sofort gewusst, dass es sich dabei um das absolute Extremum handelt. Leider ist das hier nicht der Fall. Also kommen wir um die Randpunktuntersuchung nicht herum.)

6. Schritt:Randpunktuntersuchung:

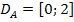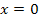Die Randpunkte der Definitionsmenge sind und 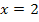. Da sie beide in der Definitionsmenge eingeschlossen sind, können wir sie einfach in die Zielfunktion einsetzen. (Ansonsten hätten wir die Grenzwerte an diesen Stellen berechnen müssen.)

Hier noch einmal die Zielfunktion: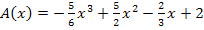

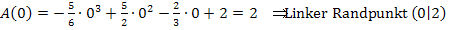
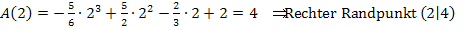
Nun vergleichen wir diese Ergebnisse mit dem Funktionswert des vorher berechneten Maximums 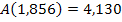. Dieser Wert ist größer als 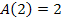und 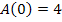. Die Randpunkte 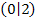und 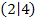liegen tiefer als der Hochpunkt  Daher liegt das absolute Maximum bei 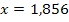. Für die maximale Fläche 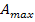gilt:

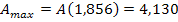
Die maximale Fläche der neuen Platte beträgt somit 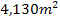. Der Glaser muss dazu im Abstand 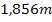vom linken Rand der ursprünglichen Glasplatte einen senkrechten Schnitt machen und einen waagrechten Schnitt in einer Höhe von 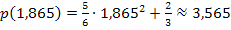Metern machen. Um die soeben genannte Schnitthöhe für den waagrechten Schnitt zu erhalten, wurde die x-Koordinate 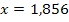in die Parabelgleichung / Nebenbedingung 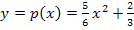eingesetzt.

Damit ist die Aufgabe gelöst. Gleich weiter mit dem nächsten Beispiel!

2. Bsp.:Minimaler Abstand

Gegeben ist die Funktion 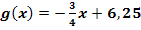. Welcher Punkt 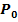der Gerade hat vom Ursprung die kleinste Entfernung? Wie lang ist dieser minimale Abstand? Löse die Aufgabe mit Hilfe der Differenzialrechnung!

Lösung:

Vorweg fertigen wir eine Zeichnung an, die den Graph der Funktion 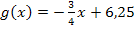und einen beliebigen Geradenpunkt P mit seinem Abstand zum Ursprung zeigt.

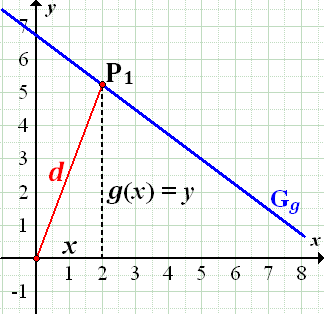
Abb.:In Blau ist der Graph 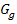der Funktion 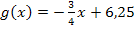dargestellt. Auf der Gerade liegen die Punkte 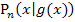. Als konkretes Beispiel für 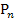ist der Punkt 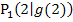und sein Abstand d zum Ursprung (in Rot) eingezeichnet.

Variablen festlegen:

x- Koordinate der Punkte 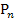:x

y-Koordinate der Punkte 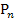:y

1. Schritt:Nebenbedingung aufschreiben

Die Punkte 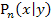liegen auf der Gerade 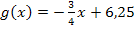bzw. 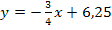. Daher gilt die Nebenbedingung: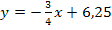

2. Schritt:Hauptbedingung aufstellen

Der Abstand von 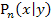zum Ursprung soll minimal werden. Wir müssen daher als Hauptbedingung eine Formel für den Abstand von 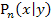zum Ursprung in Abhängigkeit von x und y aufstellen.

---