Extremwertaufgaben mit Nebenbedingung / Optimierungsprobleme

Daher gibt es in diesem Fall zwei Extrema innerhalb des Definitionsbereichs. Wir müssen also erst einmal herausfinden, welches der beiden Extrema den Hochpunkt der Zielfunktion darstellt. Außerdem muss danach noch die Randpunktuntersuchung durchgeführt werden, da ja auch einer der Randpunkte der absolute Hochpunkt sein kann. (Gäbe es nur ein einziges Extremum innerhalb der Definitionsmenge, hätte man sofort gewusst, dass es sich um das absolute Extremum handelt. Leider ist das hier nicht der Fall. Also kommen wir um die Randpunktuntersuchung nicht herum.)

Untersuchung der Art der Extrema:Welcher Punkt ist HOP bzw. TIP?

1. Methode:Mit der zweiten Ableitung (Nur für Schüler, welche die zweite Ableitung einer Funktion im Unterricht schon behandelt haben. Alle anderen verwenden stattdessen die 2. Methode.)

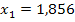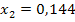Wir bilden vorweg die zweite Ableitung der Zielfunktion und setzen dann die ermittelten x-Koordinaten und in die zweite Ableitung ein. Ist das Ergebnis negativ, handelt es sich um das gesuchte Maximum.

Hier noch einmal die erste Ableitung der Zielfunktion: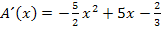 

Zweite Ableitung bilden: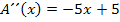

x-Koordinaten 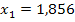und 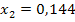jeweils einsetzten in die zweite Ableitung:

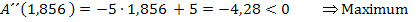
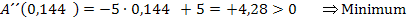
2. Möglichkeit:Untersuchung des Monotonieverhaltens der Zielfunktion

Wir wissen, dass bei 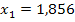und 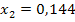Punkte mit waagrechten Tangenten vorliegen, da an diesen Stellen die erste Ableitung gleich Null ist. Nur an diesen Stellen kann sich das Vorzeichen der Ableitung ändern. Unter Berücksichtigung der Definitionsmenge 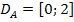fertigen wir eine Monotonietabelle an.

x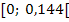
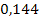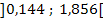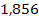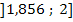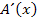		0		0

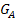Die Vorzeichen der mittleren Zeile erhalten wir, indem wir uns jeweils eine konkrete Zahl aus den drei Bereichen denken, sie in die erste Ableitung einsetzten und das Vorzeichen des Ergebnisses in die Tabelle eintragen. Man kann dazu die Ableitung in der oben genannten Form 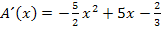verwenden oder besser die faktorisierte Form (= Produktform) .

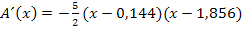Dadurch erhält man:

Nun wissen wir, dass die Zielfunktion 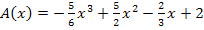bei 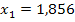einen Hochpunkt besitzt. Wir berechnen die y-Koordinate des Hochpunktes, indem wir seine x-Koordinate 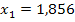in die Zielfunktion 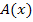einsetzen.

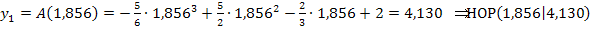
Der Funktionswert 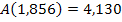muss zumindest ein relatives Maximum der Zielfunktion, also der Fläche des neuen Rechtecks sein. Ob es das absolute Maximum ist, muss noch mittels Randpunktuntersuchung herausgefunden werden.

---