Einfache Ableitungsregeln
Beachte beim Ableiten besonders:
Multiplikative Konstanten (d.h. Zahlen ohne x, die mit etwas multipliziert werden bzw. durch die dividiert wird) bleiben beim Ableiten stehen;dies besagt die Faktorregel.
Allerdings ergeben additive Konstanten (d.h. Zahlen ohne x, welche zu etwas addiert oder subtrahiert werden, in diesem Beispiel die Zahl + 3 in der Klammer) abgeleitet stets den Wert 0;daher sieht es so aus, als wenn additive Konstanten beim Ableiten wegfallen. In diesem Beispiel fällt die Zahl + 3 beim Ableiten praktisch weg, da + 3 abgeleitet + 0 ergibt und das kann man ja weglassen.
So, jetzt leiten wir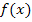 
aber endlich ab! Überlege dir 
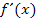gleich ´mal alleine. Das dürfte nun kein Problem mehr darstellen.
Hier noch einmal die Funktionsgleichung: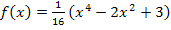 
Hast du dir 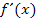selbst überlegt?
Dann müsstest du Folgendes erhalten haben:
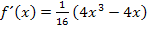
Jetzt kann man entweder 4x ausklammern oder nun doch den Bruch in die Klammer hinein multiplizieren. Es ist aber geschickter auszuklammern. Warum? Das hängt vor allem mit der Teilaufgabe b.) zusammen;dabei rechnet es sich viel besser, wenn 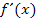zumindest teilweise faktorisiert ist. („Faktorisiert“ bedeutet „als Produkt geschrieben“. Vergleiche dazu auch Faktorisierter Funktionsterm!) Das Ausklammern führt uns hier zwar noch nicht direkt zur vollständig faktorisierten Form der Ableitung. („Vollständig faktorisiert“ bedeutet „als Produkt von Faktoren geschrieben, die nicht weiter zerlegbar sind“.) Doch liegt 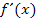nach dem Ausklammern auf jeden Fall schon einmal als Produkt vor. Warum sich die Teilaufgabe b.) damit leichter lösen lässt, wirst du gleich selbst erkennen.
Allgemein kannst du dir als Faustregel merken:Es ist in der Regel geschickter bei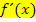 
soweit möglich auszuklammern als auszumultiplizieren.
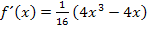
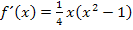
So, nun zu Teilaufgabe 7a.)
Es soll die Gleichung der Tangente an den Graph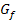 
im Kurvenpunkt 
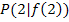ermittelt werden. Weil wir nachher die y-Koordinate von P benötigen, beginnen wir mit der Berechnung von 
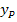. Dazu muss nur 
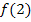berechnet werden, also in die Funktionsgleichung 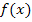für x die Zahl 2 (die gegebene x-Koordinate von P) eingesetzt werden.
Hier noch einmal die Funktionsgleichung: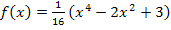
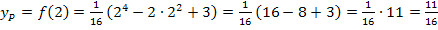
Der Kurvenpunkt P ist daher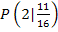 
.
Wir sollen in dieser Teilaufgabe die Tangentengleichung an den Graph 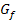im Kurvenpunkt P ermitteln. Da eine Tangente eine Gerade ist, gilt für sie die allgemeine Geradengleichung:
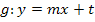
Dabei stellt m bekanntlich die Steigung und t den y-Achsenabschnitt der Geraden dar.
