Einfache Ableitungsregeln
Der entscheidende Schritt ist das Aufteilen der Wurzeln. Statt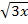 
kann man schließlich auch 
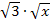schreiben. (Es gilt ja bekanntlich: 
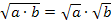) So erhält man:
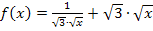
Nun schreiben wir die Wurzeln als Potenzen.
Zur Erinnerung: 
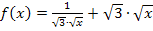
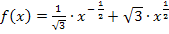
Nun lässt sich die Funktion gut ableiten.
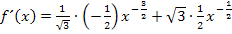
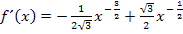
Nun formen wir die Ableitung noch so um, dass keine Brüche oder negativen Zahlen mehr in den Exponenten vorkommen. („Kosmetik“) Wir schreiben also wieder alles mit Wurzeln bzw. Brüchen.
Zur Wiederholung: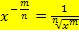 
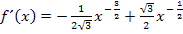
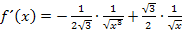
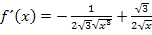
Bei dem Ausdruck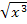 
im Nenner des ersten Bruchs kann noch teilweise radiziert werden. Das geht folgendermaßen:
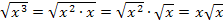
Mit dieser Umformung im Nenner des ersten Bruchs von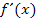 
erhält man:
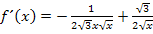
Wir bringen jetzt alles auf einen gemeinsamen Nenner. Dazu muss beim zweiten Bruch erweitert werden mit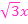 
. Das geht folgendermaßen:
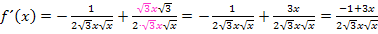
Man könnte auch noch den Nenner rational machen, d.h. so umformen, dass im Nenner keine Wurzel mehr steht. Doch das macht die Ableitung auch nicht wirklich einfacher. Daher schenken wir uns diesen Schritt.
An der letzten Teilaufgabe hast du schon einmal gesehen, dass das Ableiten nicht immer so einfach ist. Aber letztendlich ist das alles nur eine Sache der Übung.
Aus diesem Grund noch ein paar weitere Beispielaufgaben. An diesen Beispielen kannst du außerdem sehen, wofür man die Ableitung 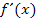verwenden kann. Nicht nur bei der Berechnung der Tangentengleichung in einem gegebenen Kurvenpunkt, sondern auch bei vielen mathematischen Problemen rund um die Steigung von Funktionen, ist die Ableitung das geeignete Mittel zum Zweck.
7. Bsp.:
Berechne zuerst die Ableitung der Funktion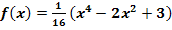 
mit Hilfe der Ableitungsregeln. Löse dann unter Verwendung von 
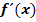die folgenden Teilaufgaben.
a.) Im Punkt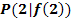 
wird die Tangente an den Graph 
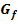gelegt. Berechne die Gleichung dieser Tangente!
b.) Ermittle, in welchen Punkten der Graph der Funktion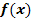 
eine waagrechte Tangente hat.
Lösung:
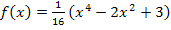
Vorweg müssen wir die Funktion ableiten. Vermutlich würdest du jetzt erst ´mal den Bruch in die Klammer hinein multiplizieren und dann ableiten. Das kannst du machen – es wäre nicht falsch - doch muss das gar nicht sein. Es geht auch einfacher! Man kann nämlich den Bruch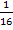 
ruhig außerhalb der Klammer stehen lassen und direkt ableiten. Beim Ableiten bleibt 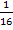dann einfach vor der Klammer stehen. 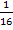ist schließlich eine multiplikative Konstante, d.h. eine Zahl ohne x, welche mit etwas (in diesem Fall mit der gesamten Klammer) multipliziert wird.
