Einfache Ableitungsregeln

Wir haben ja vorher schon gelernt, dass Zahlen, die addiert oder subtrahiert werden, beim Ableiten wegfallen. Das kann man aber auch mit der Regel 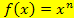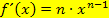begründen. Statt der Zahl 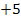denken wir uns 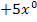. Das ergibt dann abgeleitet 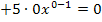. Dieselbe Regel erklärt, warum 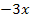abgeleitet 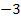ergibt. Wir denken uns beim x den Exponenten 1 dazu. Dann können wir der Reihe nach alles ableiten.

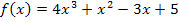
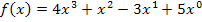
Dann folgt für die Ableitung:

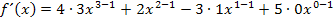
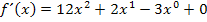
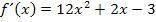
zu 5b.)

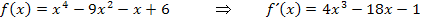
Noch nicht ganz klar? Also alles noch einmal von vorne, aber mit Zwischenschritten:

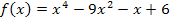
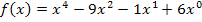
Nun bilden wir die Ableitung.

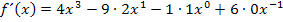
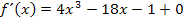
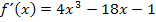
zu 5c.)

Die Zwischenschritte sparen wir uns diese Mal. Das Prinzip müsste jetzt eigentlich klar sein:Zahlen (ohne x), die addiert oder subtrahiert werden, fallen beim Ableiten komplett weg. Kommt in der Funktionsgleichung x ohne Potenz vor, bleibt in der Ableitung diejenige Zahl, die bei 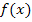vor diesem x steht, übrig. Das x fällt praktisch weg. Deshalb ergibt 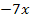abgeleitet einfach 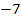. Wenn + oder – zwischen den einzelnen Faktoren steht, darf jeder Faktor einzeln abgeleitet werden.

Aber Vorsicht:Eine gleichlautende Regel für die Multiplikation oder Division gibt es dagegen nicht!

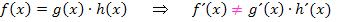
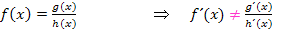
Das Produkt oder den Quotienten zweier Funktionen kannst du momentan erst dann ableiten, nachdem du ausmultipliziert bzw. dividiert hast und die Funktion dadurch auf die benötigte Form 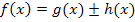gebracht hast. Später werden wir auch spezielle Ableitungsregeln für Produkte und Quotienten zweier Funktionen kennenlernen. Doch diese Regeln sind nicht mehr ganz so einfach. Daher folgen sie erst später in einem gesonderten Teil dieses Kapitels. Siehe dazu Weitere Ableitungsregeln!

Wie man auch ohne Verwendung dieser speziellen Regeln für Produkte und Quotienten etwas kompliziertere Funktionen ableiten kann, wird in der nächsten Beispielaufgabe vorgeführt.

6. Bsp.:

Differenziere die folgenden Funktionen!

a.)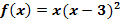

b.)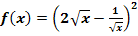

c.)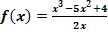

d.)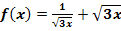

Lösung:

Hinweis:Man soll die gegebenen Funktionen differenzieren. Damit ist gemeint, dass man jeweils die Ableitung 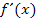bilden soll. Differenzieren ist ja nichts anderes als ableiten.

zu 6a.)

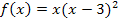
In dieser Form können wir die Funktion noch nicht ableiten. Zuerst müssen wir die Klammer auflösen. Bevor sich jedoch x in die Klammer hinein multiplizieren lässt, verwenden wir die zweite binomische Formel 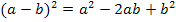, um die Klammer zu quadrieren.

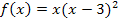
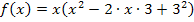
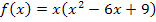
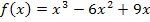
In dieser Form lässt sich die Funktion jetzt leicht ableiten. Ihre Ableitung lautet:

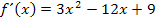
Das war doch gar nicht schwer.

---