Einfache Ableitungsregeln

Die Integralrechnung stellt somit das Gegenstück zur Differenzialrechnung dar. Ausführlich werden wir uns mit der Integralrechnung allerdings in einem gesonderten Kapitel dieser website beschäftigen. Im Unterricht werdet ihr die Integralrechnung ausführlich erst in der 12. Klasse G8 bzw. FOS/BOS besprechen. Momentan soll uns die Feststellung, dass auch die umgekehrte Rechnung von 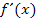zurück zu 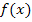bis auf eine Konstante c eindeutig ist und Integration heißt, völlig ausreichen. Mehr dazu findest du im Kapitel Einführung in die Integralrechnung.

Nun zur vierten oben gezeigten allgemeinen Ableitungsregel, der sogenannten Faktorregel:

In Worten: Eine multiplikative Konstante bleibt beim Ableiten stehen;es wird einfach der Rest der Funktion abgeleitet. Dies bedeutet, dass eine Konstante, mit der multipliziert oder durch die dividiert wird, beim Ableiten einfach stehen bleibt. Nur der Rest der Funktion wird abgeleitet. Wundere dich nicht darüber, dass in der Formel eigentlich ein Mal-Punkt steht, hier aber neben der Multiplikation mit einer Konstanten auch von der Division durch eine Konstante die Rede ist. Die Konstante c könnte schließlich auch ein Bruch sein, z.B. 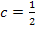. Die Multiplikation mit entspricht, wie du weißt, der Division durch die Zahl 2. Daher gilt beispielsweise: 

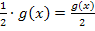
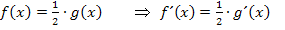
Man könnte daher für c 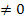auch folgende Regel aufstellen:

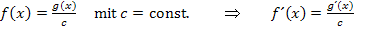
Genau genommen steckt dies aber schon in der Regel .

.

Kombiniert man die Regel, dass eine multiplikative Konstante beim Ableiten einfach stehen bleibt, mit der Regel 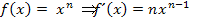, erhalten wir:

(c, n ℝ)

Das bedeutet nichts anderes, als dass du beim Ableiten die Zahl, die vor x steht, mit dem Exponenten multiplizieren und zusätzlich die Potenz um 1 verkleinern sollst.

Noch nicht ganz klar? Na, dann schauen wir uns doch einfach ein paar Beispiele an. Dann verstehst du bestimmt, wie es funktioniert.

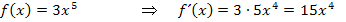
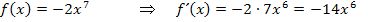
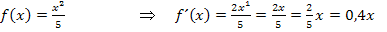
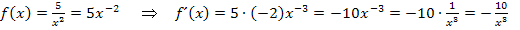
Jetzt noch zur letzten Ableitungsregel, der sogenannten Summenregel:

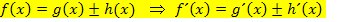
Dies bedeutet, dass Funktionen, die addiert oder subtrahiert werden, einfach nacheinander abgeleitet werden dürfen. Auch wenn man sich nicht den Kopf darüber zerbricht, macht man das eigentlich automatisch. Das wirst du gleich an den folgenden Beispielen sehen.

5. Bsp.:

Leite die folgenden Funktionen mit Hilfe der Ableitungsregeln ab!

a.)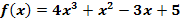

b.)

c.)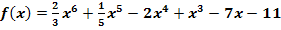

Lösung:

zu 5a.)

Zu schnell? Ok, dann alles noch einmal ganz langsam.

Die Zahl 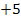fällt beim Ableiten weg, weil es sich um eine additive Konstante handelt, also um eine Zahl (ohne x), die addiert wird.

---