Einfache Ableitungsregeln

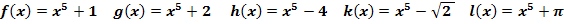
Lösung:

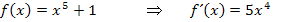
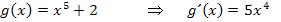
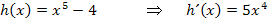
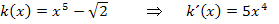
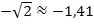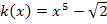Anmerkung:Die Zahl bei ist ebenfalls eine additive Konstante, weil kein x dabei vorkommt, und fällt deshalb beim Ableiten weg. Entsprechendes gilt auch für 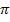in der nächsten Funktion 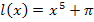. Die Kreiszahl 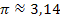ist schließlich ebenfalls eine Konstante, die addiert wird, und fällt deshalb beim Ableiten weg.

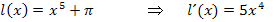
Alle hier vorkommenden Funktionen haben also die gleiche Ableitung. Die Funktionen unterscheiden sich jeweils nur in einer additiven Konstante. Das ist der Grund, warum sich immer dieselbe Ableitung ergibt. Die Graphen der Funktionen 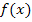bis 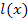gehen alle durch mehr weniger hohe Verschiebung entlang der y-Achse auseinander hervor. Die Kurven von 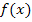bis 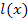haben somit alle die gleiche Form und daher an einer bestimmten Stelle auch die gleiche Steigung. Deshalb müssen alle Funktionen 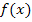bis 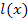dieselbe Ableitungsfunktion haben.

Wir halten noch einmal fest:Funktionen, die sich nur in einer additiven Konstante  unterscheiden, haben die gleiche Ableitung! In anderen Worten:Funktionen, deren Gleichungen sich nur in einer Zahl ohne x unterscheiden, die addiert oder subtrahiert wird, haben die gleiche Ableitung. Anschaulich bedeutet das, dass Funktionen, deren Graphen durch eine Verschiebung nach oben oder unten aufeinander abgebildet werden können, die gleiche Ableitung haben. Die y-Werte an einer bestimmten Stelle x sind zwar unterschiedlich, doch die Steigungen sind an dieser Stelle jeweils gleich.

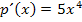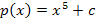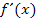Daher ist es nicht möglich, eindeutig von einer gegebenen Ableitung auf die zugehörige Funktion zu schließen. So kann die Ableitung beispielsweise von jeder Funktion der Form mit c ℝ kommen. Ohne weitere Angaben kann diese  Konstante c daher nicht explizit (d.h. genau als konkrete Zahl) ermittelt werden. Wenn man jedoch von dieser Konstante einmal absieht, ist die Rechnung von zu 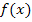allerdings schon eindeutig. Man nennt die Umkehrrechnung von 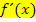zurück zu 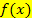integrieren. Manche Schüler sagen dazu auch „hochleiten“ oder „aufleiten“. Bitte mach das nicht! Die Begriffe „hochleiten“ bzw.  „aufleiten“ sind mathematisch nicht korrekt.

Die Rechnung, von der Funktion 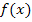zur Ableitung 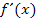, heißt zwar bekanntlich ableiten oder differenzieren. Weil sich dabei die Potenz von 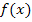um 1 verkleinert, nennt man die Berechnung von 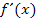ausgehend von 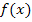eben „Ableiten“. Die Potenz geht ja herunter oder abwärts. Umgekehrt muss dann bei der umgekehrten Rechnung von 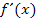zu 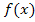, also beim Integrieren, die Potenz wieder um 1 hochgehen. Trotzdem heißt dies nicht „hochleiten“, sondern integrieren.

---