Einfache Ableitungsregeln
3. Bsp.:
Leite die Funktion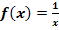 
mit Hilfe der Ableitungsregeln ab! (Hinweis:Schreibe die Funktion zuerst in der Form 
.)
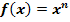Lösung:
Für die nötigen Umformungen verwenden wir, wie schon in den vorherigen Beispielen gezeigt, die Formel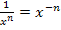 
.
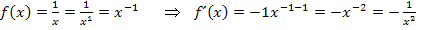
Nun zur zweiten Regel:
Jede Funktion der Form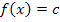 
, wobei c für eine beliebige Konstante steht, hat die Ableitung 
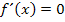. In Worten:Eine Zahl (ohne x) ergibt abgeleitet immer Null. So hat beispielsweise die Funktion 
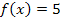die Ableitung 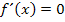. Entsprechend gilt:
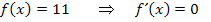
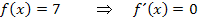
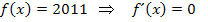
Wenn du dir überlegst, was die Ableitung einer Funktion bedeutet, wird das auch anschaulich klar. Die Ableitung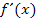 
beschreibt die Steigung der Funktion 
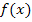. Da eine Funktion der Form 
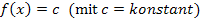eine waagrechte Gerade darstellt, welche die y-Achse in der Höhe c schneidet, muss die Steigung, also die Ableitung 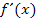, gleich Null sein. Eine waagrechte Gerade ist ja weder fallend noch steigend. Sie muss daher die Steigung Null besitzen. Somit müsste dir nun einleuchten, warum bei einer Funktion 
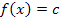für die Ableitung 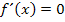gelten muss.
Die dritte Regel ergibt sich eigentlich aus der zweiten.
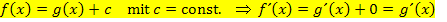
Dies bedeutet, dass eine Zahl, die addiert oder subtrahiert wird, beim Ableiten einfach wegfällt.
Wenn du dich darüber wunderst, dass dies auch für Zahlen gilt, die subtrahiert werden, obwohl in der Formel ein Plus-Zeichen vor dem c steht, bedenke Folgendes:c stellt eine beliebige reelle Konstante dar. c kann somit auch negativ sein und dies bedeutet nichts anderes, als dass eine Zahl subtrahiert wird. Die Addition einer negativen Zahl entspricht schließlich einer Subtraktion. Beispielsweise hat die Funktion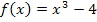 
die Ableitung 
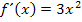. Die Zahl – 4 fällt beim Ableiten einfach weg; 
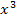wurde nach der ersten Regel 
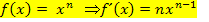abgeleitet.
Anschauliche Erklärung der Regel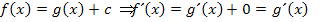 
Du weißt bestimmt, welche Auswirkung die Konstante c auf den Verlauf der Graphen von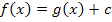 
hat:Die additive Konstante c (d.h. die Zahl ohne x, die addiert oder subtrahiert wird) verschiebt eine Funktion 
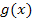nur entlang der y-Achse nach oben oder unten. Die Graphen der Funktionen 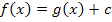gehen alle durch Verschiebung nach oben bzw. unten auseinander hervor. Diese Verschiebung verändert jedoch nichts an der Steigung der Kurve;die Form der Kurve bleibt ja gleich. Alle Graphen der Funktionen 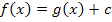müssen demnach die gleiche Steigung / Ableitung besitzen. Die additive Konstante c spielt keine Rolle für die Ableitung, sie fällt deshalb beim Ableiten weg.
4. Bsp.:
Bilde die Ableitung der folgenden Funktionen und vergleiche die Ableitungen miteinander. Was fällt dir dabei auf? Wie müssen Funktionsgleichungen aussehen, welche zu einer übereinstimmenden Ableitung führen? Kann man von der Ableitung sozusagen „rückwärts“ eindeutig auf die Funktionsgleichung schließen?
