Einfache Ableitungsregeln
Mit Hilfe dieser Regel kann man nämlich auch einfache Wurzelfunktionen oder Brüche ableiten. Man muss dazu die Funktion allerdings vorweg mit Hilfe der Potenzgesetze auf die Form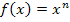 
bringen.
Wir werden uns gleich ein paar konkrete Aufgabenbeispiele dazu anschauen. Du musst dafür allerdings unbedingt die Definitionen von negativen Potenzen und Bruchpotenzen kennen. Hier noch einmal eine kurze Wiederholung der wichtigsten Definitionen solcher Potenzen. (Im Folgenden stellt x übrigens immer eine beliebige, aber positive, reelle Zahl ungleich Null dar.)
Wiederholung der wichtigsten Definitionen negativer Potenzen oder Bruchpotenzen
Formel:
Konkretes Beispiel zur jeweiligen Formel:
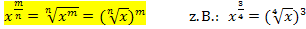
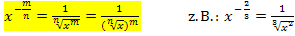
So, nun wieder zurück zur Anwendung der Ableitungsregel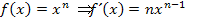 
.
1. Bsp.:
Ermittle mit Hilfe der Ableitungsregeln die Ableitung der Funktion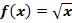 
! (Tipp:Schreibe die Wurzel als Potenz und wende dann die Ableitungsregel für 
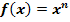an.)
Lösung:
Geg.: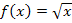 
Ges.: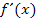 
Hinweis:Bei der „normalen“ Wurzel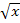 
handelt es sich genau genommen um die Quadratwurzel aus x, also um die zweite Wurzel 
.
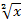Wegen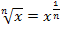 
gilt: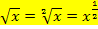 
Wenn man die Funktion 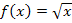anstatt mit der Wurzel in ihrer Potenzschreibweise 
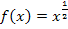schreibt, lässt sich die Ableitungsregel 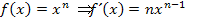anwenden.
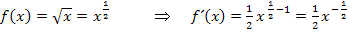
Die Ableitung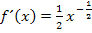 
lässt sich jedoch noch weiter vereinfachen. Im Endergebnis sollten keine negativen Exponenten oder Bruchexponenten auftreten.
Laut des Potenzgesetzes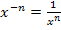 
kann folgende Umformung gemacht werden:
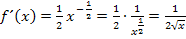
Tipp:Merke dir die Ableitung der Wurzelfunktion 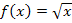auswendig. Du wirst sie später nämlich noch oft brauchen;sie steht aber nicht in der orangen bsv-Formelsammlung und auch nicht auf der Merkhilfe für G8.
Merke: 
2. Bsp.:
Leite die Funktion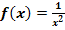 
mit Hilfe der Ableitungsregeln ab! (Hinweis:Schreibe die Funktion zuerst in der Form .)
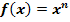Lösung:
Für die Umwandlung der Funktion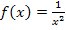 
in die Form 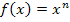verwenden wir, wie schon im 1. Bsp. gezeigt, die Formel 
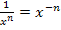. So erhalten wir:
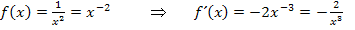
Wenn du dich jetzt wunderst, warum nicht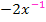 
als Ableitung herauskommt, bedenke Folgendes:Vom Exponenten der Funktion 
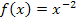, also hier der Zahl -2, muss die Zahl 1 abgezogen werden, um den Exponenten der Ableitung zu erhalten. 
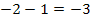, also nicht 
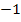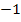! würde sich schließlich bei der Rechnung 
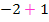ergeben;doch das sollen wir hier nicht rechnen. Jetzt noch einmal alles ganz ausführlich mit Zwischenschritt:
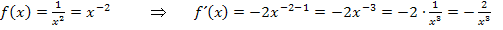
Vorsicht beim Ableiten von Potenzen mit negativem Exponenten! Wenn du von einer negativen Zahl etwas abziehst, ergibt sich etwas noch kleineres und das liegt weiter links auf dem Zahlenstrahl als die ursprüngliche Zahl.
Am besten versuchst du gleich das nächste Beispiel alleine, ohne vorher auf die Lösung zu schauen. Los geht´s!
