Vorzeichen von f’(x) fur das Monotonieverhalten graphisch ermitteln
Im 8. Bsp. soll das Monotonieverhalten der Funktion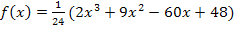 
ermittelt werden, um die Art der Extrema zu bestimmen. Dein(e) Lehrer(in) in der Schule macht dazu eine Skizze des Graphen der Ableitungsfunktion 
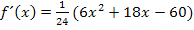und entnimmt daraus die Vorzeichen der Ableitung für die Monotonie. Wie funktioniert das genau?
1. Schritt: 
mit Hilfe der Nullstellen von 
skizzieren
Der Graph der Ableitungsfunktion ist hier eine Parabel, da die Ableitung eine quadratische Funktion ist. Die Parabel 
ist nach oben geöffnet, da die Zahl vor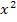 
positiv ist. (Bekanntlich sind Funktionen der Form 
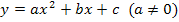Parabeln. Für 
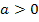liegt eine nach oben geöffnete Parabel vor. Mehr dazu bei:Quadratische Funktionen) Die Nullstellen der Ableitungsfunktion, in diesem Beispiel die Nullstellen der Parabel, haben wir oben bereits berechnet, als wir 
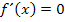berechnet haben.
Daher wissen wir:
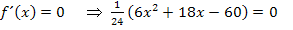
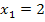
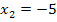
Die Nullstellen der Parabel liegen somit bei 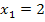und 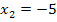. Mit Hilfe der Nullstellen können wir die Parabel 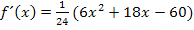grob skizzieren. Der Scheitel muss in der Mittel zwischen den Nullstellen liegen. Die y-Koordinate des Scheitels kennen wir zwar nicht, doch wir brauchen sie auch nicht unbedingt. Es reicht völlig, eine Skizze einer beliebigen nach oben geöffneten Parabel mit den Nullstellen 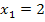und 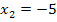zu zeichnen. Die Skizze könnte folgendermaßen aussehen:
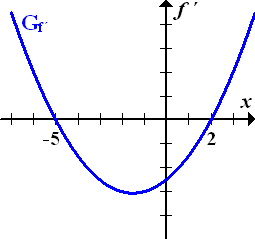
Abb.:Skizze des Graphen der Ableitungsfunktion
So weit so gut. Was hat das denn nun mit den Vorzeichen von in der Monotonietabelle zu tun? Mache dir dazu klar, dass positiv ist, wenn der Graph von oberhalb der x-Achse liegt. Umgekehrt ist negativ, wenn der Graph von unterhalb der x-Achse liegt. Wir müssen daher schauen, wo der Graph von , also unsere soeben skizzierte Parabel, oberhalb bzw. unterhalb der x-Achse verläuft. So erhalten wir die gesuchten Vorzeichen von , die wir für die Monotonieuntersuchung brauchen.
2. Schritt:Vorzeichenermittlung von mit Hilfe des Graphen
Wir ergänzen die Skizze von oben mit den jeweiligen Vorzeichen.
Plus, wenn die Ableitungsfunktion oberhalb der x-Achse liegt.
Minus, wenn sie unterhalb der x-Achse verläuft.
Das sieht dann folgendermaßen aus:
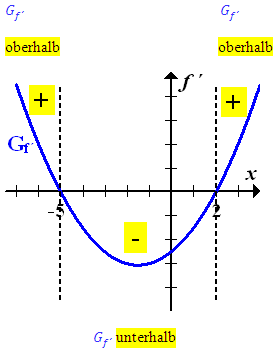
Die jeweiligen Vorzeichen können nun in die Monotonietabelle eingetragen werden.
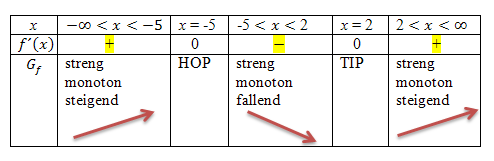
Hoffentlich ist dir nur klar geworden, wie dein(e) Lehrer(in) auf die Vorzeichen in der mittleren Zeile der Monotonietabelle kommt, obwohl er/sie keine konkreten Zahlen aus den einzelnen Bereichen in die Ableitung eingesetzt hat.
Anzumerken bleibt jedoch, dass diese graphische Methode der Vorzeichenermittlung von
nur dann gut funktioniert, wenn sich der Graph von leicht skizzieren lässt, weil es sich um eine Parabel (wie in diesem Beispiel) oder um eine Gerade handelt. Für kompliziertere Funktionen, die natürlich auch schwierigere Ableitungsfunktionen haben, ist dieses Verfahren nicht geeignet. Es empfiehlt sich dann konkrete Zahlen aus den einzelnen Bereichen einzusetzen, wie bereits oben erläutert.
