Monotonie-Intervalle angeben

Speziell für Schüler einer FOS in Bayern:Ist in einer Aufgabe verlangt, dass du die Monotonie-Intervalle einer bestimmten Funktion angeben sollst, setzt du zuerst die Ableitung gleich Null, um die x-Koordinaten aller Punkte mit waagrechten Tangenten zu berechnen. Damit fertigst du eine Monotonietabelle an. Anschließend musst du aber zusätzlich die Monotonie-Intervalle der Funktion gesondert aufschreiben;die Monotonietabelle alleine reicht nicht aus. Wie gibt man nun die Monotonie-Intervalle einer Funktion an und was ist damit überhaupt gemeint?

Die Monotonie-Intervalle einer Funktion 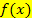sind die größtmöglichen Bereiche, wo der Graph der Funktion 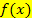streng (echt) monoton steigt bzw. wo er streng (echt) monoton fällt. (Streng monoton und echt monoton ist übrigens das Gleiche.)

Man kann die Monotonie-Intervalle im Prinzip aus der Monotonietabelle ablesen. Du suchst dazu alle Bereiche für x, wo positiv ist bzw. alle Bereiche, wo negativ ist. Bei der Angabe der jeweiligen Intervalle ist allerdings darauf zu achten, dass die Ränder der einzelnen Intervalle jeweils miteingeschlossen werden müssen! Das ist definitiv auf der FOS (nicht auf dem Gymnasium!) so verlangt, auch wenn mir dies persönlich als mathematisch unkorrekt erscheint. Warum dies meiner Meinung nach nicht der Definition gemäßkorrekt ist, das wirst du gleich sehen.

Vorweg müssen wir dazu ein paar Begriffe klären:

Laut Definition ist eine Funktion streng monoton steigend, wenn sie nur steigt, aber nicht fällt und auch keine waagrechten Tangenten besitzt. Entsprechend ist eine Funktion streng monoton fallend, wenn sie nur fällt, aber nicht steigt und keine waagrechten Tangenten besitzt. Da eine streng monotone Funktion keine waagrechten Tangenten haben kann, darf die Ableitung nicht gleich Null sein. Die Ableitung muss entweder positiv (streng monoton steigend) oder negativ (streng monoton fallend) sein.

Definition:

Eine Funktion ist in einem bestimmten Intervall I streng (echt) monoton steigend, wenn im Intervall I gilt: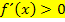

Eine Funktion ist in einem bestimmten Intervall I streng (echt) monoton fallend, wenn im Intervall I gilt: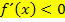

Das betrachtete Intervall I, also der jeweilige Bereich auf der x-Achse, wo die Funktion entweder nur steigt oder nur fällt, ist dabei ein offenes Intervall, das innerhalb der Definitionsmenge 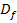der Funktion liegt. Das jeweilige Intervall I ist also ein bestimmter Bereich der Form:a <x <b oder ]a;b[

Von den Begriffen „streng monoton steigend“ bzw. „streng monoton fallend“ sind die Begriffe „monoton steigend“ bzw. „monoton fallend“ zu unterscheiden. Eine Funktion ist monoton steigend, wenn sie steigt oder waagrecht verläuft, aber eben nicht fällt. Entsprechend kann eine monoton fallende Funktion unterschiedlich stark fallen oder waagrecht verlaufen, aber eben nicht steigen. Eine monoton steigende oder monoton fallende Funktion kann also auch waagrechte Tangenten besitzen. Die Ableitung kann somit gleich Null sein.

Definition:

Eine Funktion ist in einem Intervall I monoton steigend, wenn im Intervall I gilt: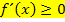

Eine Funktion ist in einem Intervall I monoton fallend, wenn im Intervall I gilt: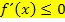

So, nun wieder zu den Monotonie-Intervallen. Schauen wir uns doch als erstes einmal an, wie du das als Schüler einer FOS schreiben sollst. Dann besprechen wir, ob das mit der Definition vereinbar ist.

Gehen wir zurück zu unserem Beispiel der Funktion .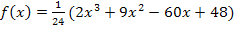

Aus 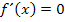hat sich ergeben: 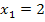und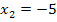

Die fertige Monotonietabelle sah in diesem Beispiel folgendermaßen aus:

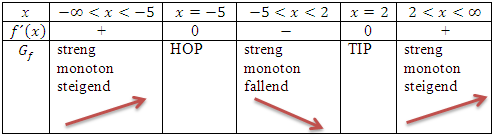
Die Monotonie-Intervalle der Funktion sollen dann auf der FOS, nicht aber auf dem Gymnasium, folgendermaßen angegeben werden:

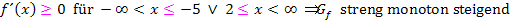
Alternativ dazu kann auch auf der FOS die Intervallschreibweise verwendet werden:

Monotonietabelle:

x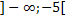
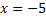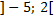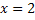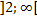	+	0		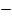0	+
	str. m. steigend	HOP	str. m. fallend	TIP	str. m. steigend

Die Monotonie-Intervalle von lauten in der Intervallschreibweise:

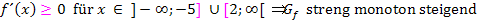
Genauso wie es gerade gezeigt wurde, musst du das als Schüler einer FOS in Bayern schreiben. Es muss definitiv 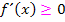bzw. 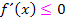und nicht 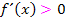bzw. 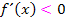geschrieben werden;entsprechend müssen die Zahlen -5 und 2 tatsächlich eingeschlossen werden. Jeweils dahinter soll entsprechend „ ist streng (echt) monoton steigend bzw. fallend“ geschrieben werden. So ist das auf der FOS verlangt. Wenn man es anders macht, gibt es Punktabzug! Doch liegt genau darin das Problem:Wenn man die Ränder -5 und 2 einschließt, dann hat die Funktion an genau diesen Stellen des Intervalls waagrechte Tangenten und die Ableitung ist an diesen Stellen gleich Null. Dann ist die Funktion aber laut Definition nicht mehr streng monoton steigend bzw. fallend, sondern nur monoton steigend bzw. fallend. Daher leuchtet mir persönlich die auf der FOS geforderte Schreibweise der Monotonie-Intervalle nicht ein. Normalerweise ist schließlich bei dem Begriff „streng monoton“ immer von einem offenen Intervall I die Rede. Vergleiche Definition oben! Ich kann dir daher leider nicht erklären, warum alle Schüler einer FOS bei den Monotonie-Intervallen die Ränder einschließen müssen und trotzdem streng monoton steigend / fallend dahinter schreiben sollen. (Gymnasiasten würden es dagegen tatsächlich als Fehler angestrichen bekommen, wenn sie die Ränder bei den Monotonie-Bereichen einschließen würden.)

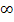Trotzdem gilt für alle Schüler einer FOS:Bei den Monotonie-Intervallen sind die Ränder grundsätzlich einzuschließen, mit Ausnahme von und . ( und 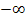werden schließlich immer ausgeschlossen, weil es sich dabei um keine reellen Zahlen handelt.)

---