Genauere Erklarungen zum graphischen Differenzieren
Entweder ist der Funktionsgraph einer Funktion 
gegeben, aber keine Funktionsgleichung, oder es ist die Gleichung von angegeben. Sollst du dann die Funktion graphisch differenzieren (ableiten), heißt das entweder, dass du die Tangentensteigung an einer bestimmten Stelle graphisch ermitteln sollst oder, dass du den Graph der ganzen Ableitungsfunktion ohne vorherige Rechnung zeichnen sollst. Das hängt davon ab, ob ein konkreter Punkt angegeben ist, wo differenziert werden soll, oder nicht.
Soll die Tangentensteigung von in einem bestimmten Punkt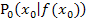 
ermittelt werden, heißt das „lokales Differenzieren“. Wenn die gesamte Ableitungsfunktion gezeichnet werden soll, spricht man allgemein von „globalem Differenzieren“.
Beim „graphischen Differenzieren“ soll man die Tangentensteigung einfach aus einer Zeichnung ablesen. Die Steigung der jeweiligen Tangente entspricht dann der Steigung der Funktion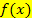 
im Berührpunkt mit der Tangente. Das graphische Differenzieren ist natürlich ziemlich ungenau, aber besser geht es nur rechnerisch.
1. Lokales Differenzieren (graphisch)
Du brauchst dazu den Graph 
der Funktion . Entweder ist er schon gegeben oder du musst ihn z. B. mit einer Wertetabelle selbst zeichnen. Gegeben ist auf jeden Fall ein Kurvenpunkt 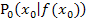, in dem die Tangentensteigung / die Steigung der Funktion ermittelt werden soll.
Nun musst du so genau wie möglich im Punkt 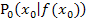die Tangente an zeichnen und die Steigung aus der Zeichnung ablesen. Die Steigung ermittelst du dabei folgendermaßen:Zeichne ein Steigungsdreieck an die Tangente, indem du von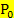 
ausgehend um 1 nach rechts und dann senkrecht nach oben bzw. unten bis zu einem anderen Punkt der Tangente gehst. Messe dann so genau wie möglich die Länge der Strecke ab, die du senkrecht nach oben bzw. unten gegangen bist. Diese senkrechte Länge ergibt die Tangentensteigung, wobei das Vorzeichen der Steigung positiv ist, wenn du nach oben gegangen bist, und entsprechend negativ, wenn du nach unten gegangen bist.
Du kannst das Steigungsdreieck auch größer zeichnen. Wenn du aber statt 1 nach rechts einen anderen Wert nach rechts gehst, musst du diejenige Länge, welche du senkrecht nach oben bzw. nach unten gegangen bist, noch durch die Länge dividieren, die du nach rechts gegangen bist. Also einfach senkrechte Länge durch waagrechte Länge teilen, um die Steigung aus dem Steigungsdreieck zu ermitteln! Auch dadurch erhältst du die Steigung.
Das Vorzeichen der Steigung ist dabei positiv, wenn du nach rechts und dann nach oben gegangen bist, bzw. negativ, wenn du nach rechts und dann nach unten gegangen bist. Würdest du nach links gehen beim Zeichnen des Steigungsdreiecks, würde sich alles umkehren. Daher ist davon allgemein abzuraten. Irgendwie ist es doch logischer, dass ein positives Vorzeichen kommt, wenn man nach oben geht, und ein negatives Vorzeichen, wenn man nach unten geht. Das stimmt aber nur, solange man nach rechts geht. Also besser immer nach rechts gehen beim Steigungsdreieck!
Bsp.: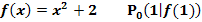 
Es soll die Tangentensteigung in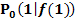 
graphisch ermittelt werden.
Lösung:
Wir zeichnen zuerst den Graph der Funktion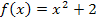 
. Es handelt sich dabei um eine nach oben geöffnete Normalparabel, die um 2 nach oben verschoben ist. Dann zeichnen wir so genau wie möglich im angegebenen Kurvenpunkt 
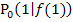die Tangente an den Graph . Als letztes zeichnen wir ein Steigungsdreieck an die Tangente und lesen daran die Steigung ab. (Das Steigungsdreieck ist in der folgenden Abbildung in Rot gezeichnet.)
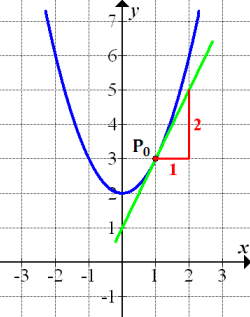
Abb.:Graph der Funktion 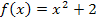und Tangente in 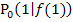mit Steigungsdreieck
Man erkennt in der Abbildung, dass die Steigung der Tangente im Punkt 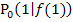den Wert 2 hat, weil man 1 nach rechts und 2 nach oben gegangen ist. Es gilt somit:
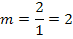
Daher hat die Parabel 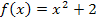im Punkt 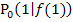ebenfalls die Steigung 2. Es gilt für die Ableitung an der Stelle 
:
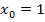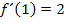
Die Ableitung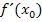 
ist schließlich nichts anderes als die Steigung der Funktion an der jeweiligen Stelle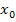 
bzw. die Tangentensteigung im entsprechenden Punkt .
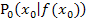Hinweis:
Das Steigungsdreieck hättest du auch größer z.B. mit 2 nach rechts und 4 nach oben zeichnen können. Dann hättest du die Steigung mit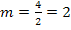 
berechnet. Dabei ergibt sich natürlich das gleiche wie oben mit 
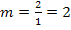. Bei der Steigung geht es ja nur um das Verhältnis der senkrechten zur waagrechten Strecke des Steigungsdreiecks. Das Verhältnis 4 :2 ist logischerweise das gleiche wie 2 :1.
Wie weit du beim Steigungsdreieck nach rechts gehst, ist somit an sich egal. Aber besonders praktisch ist es eben, wenn man genau um 1 nach rechts geht, weil dann die Länge der senkrechten Strecke direkt der Steigung m entspricht.
2. Graphisches Differenzieren (global, also nicht nur in einem Punkt)
Gegeben ist nur der Graph einer Funktion , aber nicht ihre Funktionsgleichung. Du sollst den Graph der gesamten Ableitungsfunktion 
zeichnen. Dabei musst du die Steigung der Funktion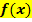 
an einer bestimmten Stelle x als Funktionswert y der Ableitungsfunktion 
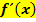auffassen. Das wird unten gleich noch an einem konkreten Beispiel gezeigt. Die Steigung der Funktion entspricht bekanntlich der Tangentensteigung an der entsprechenden Stelle. Um den Graph der Ableitungsfunktion möglichst genau zeichnen zu können, muss man an möglichst vielen Stellen jeweils die Steigung der Tangente an den Funktionsgraph 
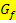aus der Zeichnung ablesen. Dabei gehst du jeweils folgendermaßen vor:
Tangentensteigung aus einer Zeichnung ablesen:
· Wähle eine bestimmte Stelle x = a, beispielsweise x = 0,5. (Das ist ein absolut willkürlich gewähltes Zahlenbeispiel.)
· Zeichne im Kurvenpunkt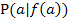 
, also in unserem Beispiel 
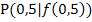, so genau wie möglich die Tangente an den gegebenen Funktionsgraphen .
· Zeichne ein Steigungsdreieck der Tangente ein, indem du von P ausgehend um 1 nach rechts und dann senkrecht nach oben bzw. unten bis zu einem anderen Punkt der Tangente gehst. Messe dann so genau wie möglich die Länge der Strecke ab, die du nach oben bzw. unten gegangen bist. Diese senkrechte Länge ergibt die Tangentensteigung, wobei das Vorzeichen der Steigung positiv sein muss, wenn du nach oben gegangen bist, und entsprechend negativ, wenn du nach unten gegangen bist. (Du kannst das Steigungsdreieck auch größer zeichnen, man muss dabei also nicht unbedingt genau 1 nach rechts gehen. Wenn du aber stattdessen einen anderen Wert nach rechts gehst, musst du die Länge, die du senkrecht nach oben bzw. nach unten gegangen bist, noch durch die Länge dividieren, die du nach rechts gegangen bist. Dann also immer senkrechte Länge durch waagrechte Länge teilen, um die Steigung zu ermitteln! Darauf wurde schon beim lokalen Differenzieren näher eingegangen.)
Die an der Stelle x = a ermittelte Tangentensteigung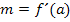 
entspricht dann der y-Koordinate des Punktes P´auf der Ableitungsfunktion. Der Punkt P´hat also die Koordinaten x = a und y = m.
In der folgenden Abbildung wurde die Steigung von an der Stelle x = 1 graphisch ermittelt. Aus der Zeichnung ergibt sich in diesem Beispiel eine Tangentensteigung von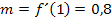 
. Der zugehörige Punkt P´auf dem Graph 
der Ableitungsfunktion lautet somit P´(1|0,8).
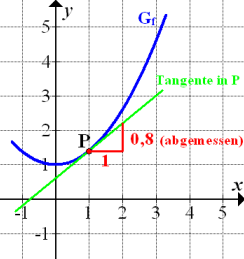
Abb.:Graph einer Funktion mit Tangente im Punkt P und Steigungsdreieck
Entsprechend geht man dann an möglichst vielen weiteren Stellen vor, so dann man letztendlich genügend Punkte der Ableitungsfunktion weiß, um den Graph der Ableitungsfunktion skizzieren zu können.
Mehr zum Thema Ableitungsfunktion erst später im gesonderten Teil: Die Ableitungsfunktion
