b.) Zusammenhang der Funktion f (x) mit ihrer Ableitungsfunktion f´(x)
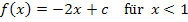
Die Zahl c lässt sich dabei nicht ermitteln. Das haben wir oben ja schon besprochen.
Nun zum nächsten Teil der Ableitungsfunktion:
Für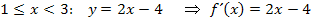 
Auf die Gleichung der Ableitungsfunktion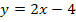 
kommst du mit Hilfe der Abbildung. Es handelt sich im Bereich 
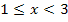bei der Ableitungsfunktion schließlich um eine Gerade und lineare Funktionen/Geraden haben die allgemeine Gleichung y = mx + t. Du kannst m und t aus der Abbildung von 
ablesen. Am besten ist es, wenn du dir den Graph der Ableitungsfunktion selbst auf ein Papier zeichnest. Dann kannst du diesen Teil des Graphen (die steigende Gerade) entsprechend verlängert einzeichnen, so dass du den y-Achsenabschnitt t besser ablesen kannst. Du wirst sehen, dass die y-Achse genau bei y = -4 geschnitten wird, daher gilt t = -4. Auch die Steigung m der steigenden Geraden lässt sich leicht ablesen, wenn du dir ein Steigungsdreieck einzeichnest. Man geht dabei am besten 1 nach rechts und 2 nach oben. Daher gilt:m =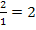 
(Vorsicht:Es handelt sich hierbei um die Steigung der Ableitungsfunktion und noch nicht um die Steigung der Funktion 
. Wir sind ja gerade dabei die Gleichung der Ableitungsfunktion zu ermitteln, damit wir uns nachher Gedanken über die Funktionsgleichung von machen können.)
So könnte deine Zeichnung aussehen:
(Das Steigungsdreieck ist in Rosa dargestellt;gestrichelt die nötige Verlängerung der steigenden Geraden, damit man t besser ablesen kann.)
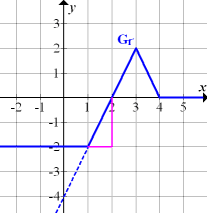
Wie kommt man nun von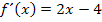 
auf ? Das Integrieren, also rückwärts von der Ableitung zur Funktion zu rechnen, haben wir noch nicht besprochen. Auch dafür gibt es natürlich Regeln, doch die kennst du momentan vermutlich noch nicht. Versuche trotzdem gleich ´mal alleine auf die Gleichung von zu kommen. Bei diesem Beispiel ist das auch wirklich nicht so schwer.
Hast du es dir selbst überlegt?
Dann müsstest du darauf gekommen sein, dass eine Parabel mit der folgenden Gleichung sein muss:
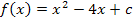(c kann man hier natürlich nicht ermitteln.)
Solltest du noch Schwierigkeiten gehabt haben, ausgehend von 
zu ermitteln, hier ein kleiner Tipp:Zähle zum Exponenten bei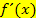 
die Zahl 1 dazu, das ergibt den Exponenten von 
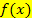, und dividiere außerdem durch den neuen Exponenten. So erhältst du 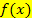. Dies heißt, wie gesagt, integrieren. Wir kommen später noch einmal darauf zurück. (Dann wird das auch ausführlich erklärt.) Als Formel sieht das Ganze folgendermaßen aus:
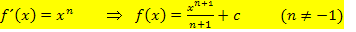
Auf unser Beispiel angewendet, bedeutet das:
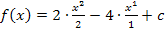
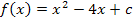
Um diese Aufgabe zu lösen, hätte man die Funktionsgleichung von gar nicht unbedingt ermitteln müssen. Doch es hat sich so schön als Einführung in die Integralrechnung verwenden lassen. Außerdem fällt es dir so bestimmt leichter zu erkennen, dass der Funktionsgraph 
zwischen x = 1 und x = 3 ein Teil einer nach oben geöffneten Normalparabel sein muss. Die x-Koordinate ihres Scheitels lässt sich leicht aus dem Graph der Ableitungsfunktion ablesen. Bei x = 2 hat eine Nullstelle (mit Vorzeichenwechsel). D.h.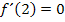 
und das bedeutet für den gesuchten Graph , dass bei x = 2 die Steigung der Tangente von gleich Null sein muss, also dass dort eine waagrechte Tangente haben muss. Daher ist bei x = 2 ein Extremum, was nichts anderes als der Scheitel ist. Der Scheitel hat somit die x-Koordinate x = 2. Da die Ableitungsfunktion für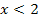 
unterhalb der x-Achse liegt, ist hier negativ, also ist für 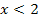streng monoton fallend. Für 
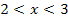liegt die Ableitungsfunktion oberhalb der x-Achse, deshalb ist hier positiv und in diesem Bereich streng monoton steigend.
