b.) Zusammenhang der Funktion f (x) mit ihrer Ableitungsfunktion f´(x)

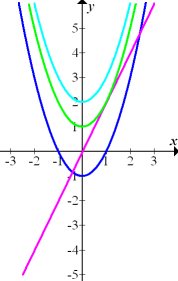
Abb.:Die Graphen von 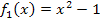in Blau, 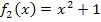in Grün, 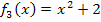in Hellblau und in Rosa ihre gemeinsame Ableitungsfunktion .

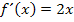Die Ableitung 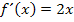könnte theoretisch von jeder Funktion der Form 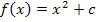kommen. Oder anders herum:Alle Funktionen der Form 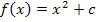sind Stammfunktionen der Ableitungsfunktion 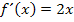. Wenn nur die Ableitung 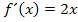gegeben ist, kann man die additive Konstante c nicht eindeutig bestimmen.

Daher kann man ohne weitere Angaben nicht eindeutig vom Graphen der Ableitungsfunktion auf den Graph von schließen.

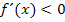Man kann zwar sagen, dass fallen muss, wo unterhalb der x-Achse verläuft und somit gilt.

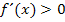Außerdem weißman, dass steigen muss, wo oberhalb der x-Achse verläuft und somit gilt.

Hat an der Stelle 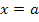eine Nullstelle mit Vorzeichenwechsel, muss bei 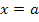ein Extremum besitzen, doch kann man nicht auf die y-Koordinate des Extremums kommen.

beschreibt schließlich nur das Monotonieverhalten (Steigungsverhalten) von . Man kann somit die „Form“ von aus erschließen, aber nicht in welcher „Höhe“ der Graph liegt. Eine Ableitungsfunktion kann deshalb zu verschiedenen Funktionen gehören, deren Graphen alle mehr oder weniger entlang der y-Achse nach oben oder unten verschoben sind.

2. Bsp.:

In der folgenden Abbildung ist der Graph der Ableitung 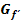dargestellt. Was lässt sich damit über den Graph der Funktion 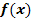aussagen? Skizziere den Verlauf eines Graphen , der zur gezeigten Ableitungsfunktion gehören kann!

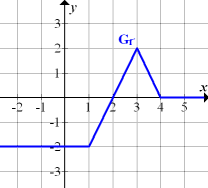
Lösung:

Es soll ausgehend vom Graph der Ableitungsfunktion auf den Verlauf des Funktionsgraphen einer unbekannten Funktion geschlossen werden. Dafür muss man sich folgendes bewusst machen:Der Funktionswert der Ableitungsfunktion (also die y-Koordinate eines Punktes von 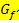) entspricht der Steigung der Funktion 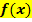an dieser Stelle.

Nehmen wir beispielsweise den Punkt (3|2). Weil er auf der Ableitungsfunktion liegt, bekommt er eine Bezeichnung mit einem Strich. Nennen wir diesen Punkt  P´(3|2). Die Koordinaten von P´verraten uns, dass der Graph der gesuchten Funktion an der Stelle x = 3 die Steigung 2 haben muss. Wie hoch die Funktion liegt, kann man nicht sagen. Die y-Koordinaten der Punkte von lassen sich nur mit nicht angeben!

Nehmen wir noch einen anderen Punkt von , der sich gut ablesen lässt, um den Zusammenhang von mit wirklich klar zu machen, beispielsweise den Punkt Q´(1,5|-1). Überlege dir doch gleich ´mal selbst, was dies für den Graph bedeutet!

Hast du es dir inzwischen alleine überlegt, was man aus Q´(1,5|-1) schließen kann?

---